Lançamento Vertical

O lançamento vertical é um movimento unidimensional no qual se desconsidera o atrito com o ar. Esse tipo de movimento ocorre quando um corpo é lançado na direção vertical e para cima. O movimento descrito pelo projétil é retardado pela aceleração da gravidade até que ele atinja a sua altura máxima. Após essa altura, o movimento passa a ser descrito como uma queda livre.

Veja também: O que é gravidade?

Tópicos deste artigo

• 1 - Fórmulas do lançamento vertical
• 2 - Queda livre
• 3 - Lançamento horizontal e oblíquo
• 4 - Exercícios de lançamento vertical e queda livre

Fórmulas do lançamento vertical

As leis que explicam o movimento dos corpos que sem movem na direção vertical foram descobertas e enunciadas pelo físico italiano Galileu Galileu. Na ocasião, Galileu percebeu que corpos de massas diferentes devem cair com o mesmo tempo e com aceleração constante em direção ao solo. Essa situação só não será possível caso a força de resistência do ar atue sobre esses corpos, dissipando sua velocidade.

O lançamento vertical é um caso particular de movimento uniformemente variado (MUV), já que ocorre sob a ação de uma aceleração constante. Nesse caso, a aceleração da gravidade opõe-se à velocidade de lançamento do projétil, que tem sentido positivo.

As equações que regem esse tipo de movimento são as mesmas utilizadas para os casos gerais do MUV, sujeitas a pequenas alterações de notação. Confira:

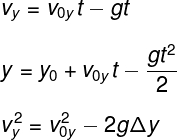
Essas são as três equações mais úteis para a descrição do lançamento vertical: funções horárias da velocidade e da posição e equação de Torricelli.

Nas equações acima, v_y é a altura final atingida pelo projétil para um dado instante de tempo t. A velocidade inicial v_0y é a velocidade com que o projétil é lançado, podendo ser positiva, caso o lançamento seja para cima, ou negativa, caso o lançamento seja para baixo, ou seja, a favor da gravidade. As alturas final e inicial do lançamento são chamadas, respectivamente, de y e y_0. Por fim, g é a aceleração da gravidade no local do lançamento.

É importante lembrar que as equações acima são definidas de acordo com o Sistema Internacional de Medidas (SI), portanto, as velocidades são dadas em m/s; a gravidade, em m/s²; e o tempo, em segundos.

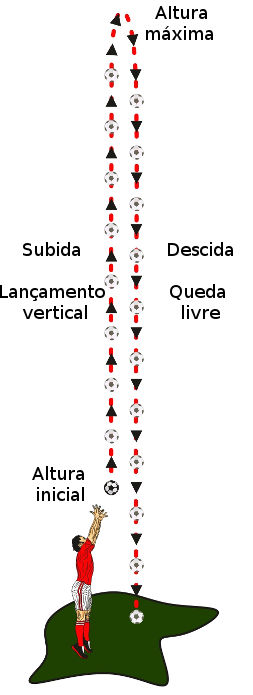
Etapas do movimento de lançamento vertical e da queda livre de uma bola

As equações acima podem ser usadas para resolver problemas envolvendo o lançamento vertical de projéteis. O referencial escolhido para essas equações adota como positivo o sentido para cima e como negativo o sentido para baixo.

→ Função horária da velocidade

A primeira das equações mostradas é a função horária da velocidade para o lançamento vertical. Nela, temos a velocidade final (v_y), a velocidade de lançamento do projétil (v_0y), a aceleração da gravidade (g) e o tempo (t):

Por meio da equação acima, podemos determinar o tempo de subida do projétil. Para tanto, devemos lembrar que, ao atingir a sua altura máxima, a velocidade vertical (v_y) é nula. Além disso, o movimento muda de sentido, passando a descrever uma queda livre. Assumindo que a velocidade vertical (v_y) é nula no ponto mais alto do lançamento vertical, teremos a seguinte igualdade:

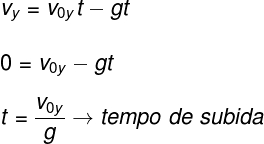
→ Função horária da posição

A segunda equação mostrada na imagem é chamada de função horária da posição. Essa equação permite encontrar em qual altura (y) um projétil estará em um determinado instante de tempo (t). Para isso, devemos saber de qual altura o projétil foi lançado (H) e com qual velocidade ocorreu o lançamento (v_0y). Se substituirmos o tempo de subida nas variáveis t nessa equação, é possível estabelecer uma relação entre a altura máxima atingida e a velocidade de lançamento do projétil (v_0y). Veja:

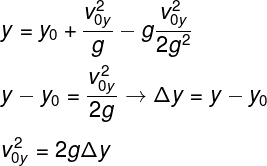
O mesmo resultado mostrado acima pode ser obtido se utilizarmos a equação de Torricelli. Para isso, basta substituirmos o termo da velocidade final por 0, uma vez que, como dito anteriormente, no ponto mais alto do lançamento vertical, essa velocidade é nula.

Queda livre

Quando um projétil lançado verticalmente atinge sua altura máxima, inicia-se o movimento de queda livre. Nesse movimento, o projétil cai em direção ao solo com aceleração constante. Para definirmos as equações desse tipo de movimento, é interessante definir um referencial favorável à aceleração da gravidade. Para isso, adotamos o sentido para baixo como positivo e consideramos que a posição inicial do movimento de queda livre é 0. Dessa forma, as equações para a queda livre tornam-se mais simples. Observe:

Lançamento horizontal e oblíquo

O lançamento horizontal e oblíquo são outros tipos de lançamento de projétil. Nesses casos, a diferença fica por conta do ângulo do lançamento em relação ao solo. Confira nossos artigos que tratam especificamente sobre o lançamento horizontal e o lançamento oblíquo:

• Lançamento horizontal no vácuo

• Lançamento oblíquo

Exercícios de lançamento vertical e queda livre

1) Um projétil de 2 kg é lançado verticalmente para cima, a partir do solo, com velocidade de 20 m/s. Determine:

Dados: g = 10 m/s²

a) o tempo total de subida do projétil.

b) a altura máxima atingida pelo projétil.

c) a velocidade do projétil nos instantes t = 1,0 s e t = 3,0 s. Explique o resultado obtido.

Resolução

a) Podemos calcular o tempo de subida do projétil usando uma das equações mostradas ao longo do texto:

Para usar essa equação, é preciso lembrar que, no ponto de altura máxima, a velocidade final do projétil é nula. Como foi informado pelo exercício, a velocidade de lançamento do projétil é de 20 m/s. Dessa forma:

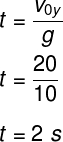
b) Sabendo o tempo necessário para o projétil atingir sua altura máxima, podemos calcular facilmente essa altura. Para isso, utilizaremos a seguinte relação:

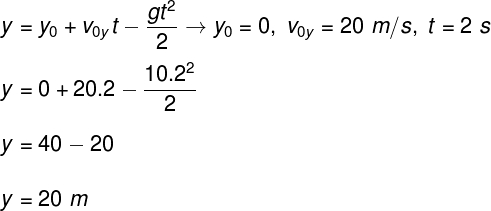
No cálculo acima, levamos em conta que o projétil foi lançado a partir do solo, por isso, y₀ = 0.

c) Podemos calcular facilmente a velocidade do projétil para os instantes t = 1,0 s e t = 3,0 s usando a função horária da velocidade. Observe:

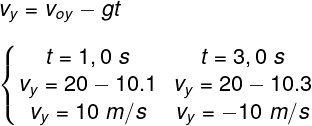
Feitos os cálculos, encontramos os valores de 10 m/s e de -10 m/s para os instantes de tempo t = 1,0 s e t = 3,0 s, respectivamente. Isso indica que, no tempo de 3,0 s, o projétil encontra-se na mesma altura que no tempo de 1,0 s. No entanto, o movimento ocorre em sentido contrário, uma vez que o tempo de subida desse projétil é de 2,0 s. Após a passagem desse intervalo de tempo, o projétil inicia seu movimento de queda livre.

Por Me. Rafael Helerbrock