Equação de Torricelli

A equação de Torricelli é uma das equações da cinemática para o movimento uniformemente variado (MUV), no qual a velocidade varia com o tempo sob aceleração constante. Desenvolvida pelo físico Evangelista Torricelli, essa equação é útil na resolução de problemas quando a variável tempo não é fornecida.

Leia também: O que se estuda em cinemática?

Tópicos deste artigo

• 1 - Resumo sobre equação de Torricelli
• 2 - Videoaula sobre equação de Torricelli
• 3 - O que é a equação de Torricelli?
• 4 - Fórmula de Torricelli
• 5 - Como calcular a equação de Torricelli?
• 6 - Gráfico da equação de Torricelli
• 7 - Para que serve a equação de Torricelli?
• 8 - Exercícios resolvidos sobre equação de Torricelli

Cinemática

Saiba mais

Como resolver exercícios de Cinemática?

Saiba mais

Resumo sobre equação de Torricelli

• A equação de Torricelli é uma equação da cinemática aplicada ao movimento uniformemente variado (MUV).
• Foi desenvolvida no século XVII pelo físico italiano Evangelista Torricelli.
• É expressa por: $v^2 = v_0^2 + 2 \cdot a \cdot \Delta s$.
• Deriva das equações horárias do MUV, eliminando a variável tempo.
• É útil para resolver problemas de cinemática que envolvem deslocamento, velocidade e aceleração sem a necessidade de considerar o tempo.

Videoaula sobre equação de Torricelli

O que é a equação de Torricelli?

A equação de Torricelli é uma das equações da cinemática, mais especificamente do movimento uniformemente variado (MUV) — os movimentos que têm velocidades que variam no tempo, com aceleração constante. Ela foi desenvolvida pelo físico italiano Evangelista Torricelli no século XVII e é muito utilizada até os tempos atuais pelos cientistas, engenheiros e outros profissionais que precisam se valer das leis da mecânica clássica.

Fórmula de Torricelli

A fórmula da equação de Torricelli é dada por:

$v^2 = v_0^2 + 2 \cdot a \cdot \Delta s$

• v → velocidade final, medida em [m/s].

• v₀ → velocidade inicial, medida em [m/s].

• a → aceleração, medida em [m/s²].

• Δs → variação do deslocamento, medida em [m].

Veja também: Como é calculada a velocidade média?

Como calcular a equação de Torricelli?

Na equação $v=v_0+a \cdot t$, isolando o tempo t, obtemos:

$t = \frac{v - v_0}{a}$

Substituindo essa expressão na equação $\Delta s = v_0 \cdot t + \frac{a}{2} \cdot t^2$, obtemos:

$\Delta s = v_0 \left( \frac{v - v_0}{a} \right) + \frac{a}{2} \left( \frac{v - v_0}{a} \right)^2$

$\Delta s = \frac{v \cdot v_0 - v_0^2}{a} + \frac{a}{2} \left( \frac{v^2 - 2 \cdot v \cdot v_0 + v_0^2}{a^2} \right)$

$\Delta s = \frac{v \cdot v_0}{a} - \frac{v_0^2}{a} + \frac{v^2}{2 \cdot a} - \frac{v \cdot v_0}{a} + \frac{v_0^2}{2 \cdot a}$

$\Delta s = \frac{v^2}{2 \cdot a} - \frac{v_0^2}{2 \cdot a}$

$2 \cdot a \cdot \Delta s = v^2 - v_0^2$

Com isso, encontramos a equação de Torricelli:

$v^2 = v_0^2 + 2 \cdot a \cdot \Delta s$

Gráfico da equação de Torricelli

O gráfico abaixo representa um típico movimento uniformemente variado (MUV), em que a velocidade muda com o tempo de forma constante. Isso é um indicativo de que a aceleração não varia com relação ao tempo. Portanto, é o gráfico de uma função que obedece às equações do MUV.

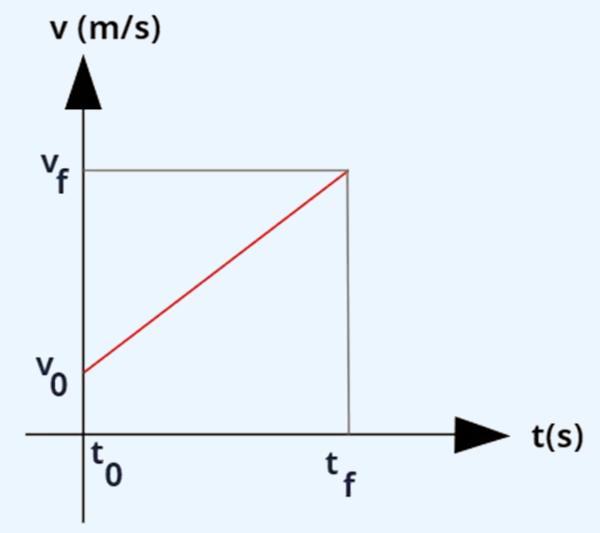
• t₀ → tempo inicial, medido em [s].
• t_f → tempo final, medido em [s].
• v_o → velocidade inicial, medida em [m/s].
• v_f → velocidade final, medida em [m/s].

Note que a função velocidade é crescente, ou seja, aumenta com o passar do tempo, logo, é uma aceleração positiva.

Para que serve a equação de Torricelli?

A equação de Torricelli é de grande utilidade na resolução de exercícios que apresentam como dados o deslocamento, a velocidade e a aceleração, sem mencionar o tempo.

Saiba mais: 10 equações da Física que são fundamentais para o Enem

Exercícios resolvidos sobre equação de Torricelli

Questão 1 Um carro se movimenta com velocidade constante de 30 m/s. Ao se deparar com um animal na pista, o motorista pisa no freio uniformemente e percorre 50 m até parar. Determine a aceleração produzida pelos freios.

A) - 9 m/s²

B) 9 m/s²

C) 0

D) - 5 m/s²

E) 5 m/s²

Resolução:

Alternativa A

Usando a equação de Torricelli:

$v^2 = v_0^2 + 2 \cdot a \cdot \Delta s$

$0 = 30^2 + 2 \cdot a \cdot 50$

$100 \cdot a=-900$

$a=-9 m⁄s^2$

Questão 2 (ESPM-SP) Um móvel percorre 180 m partindo do repouso. Se o móvel tem aceleração constante de 1,6 m/s², qual será a sua velocidade no final do trajeto?

A) 24 m/s

B) 36 m/s

C) 48 m/s

D) 60 m/s

E) 72 m/s

Resolução:

Alternativa A

Usando a equação de Torricelli:

$v^2 = v_0^2 + 2 \cdot a \cdot \Delta s$

$v^2 = 0 + 2 \cdot 1,6 \cdot 180$

$v^2=576$

$v=24 \ m/s$

Fontes

CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica (vol. 1). 9 ed. Rio de Janeiro, RJ: LTC, 2012.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.