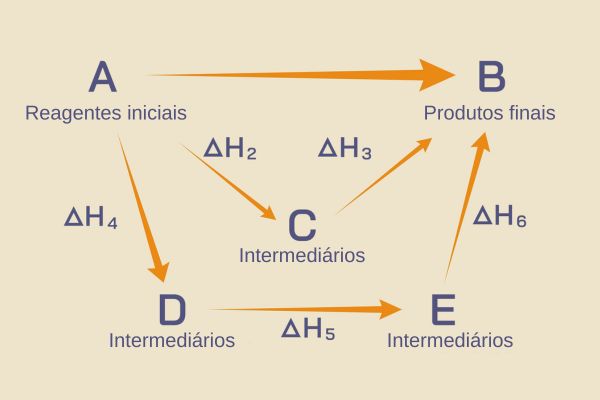
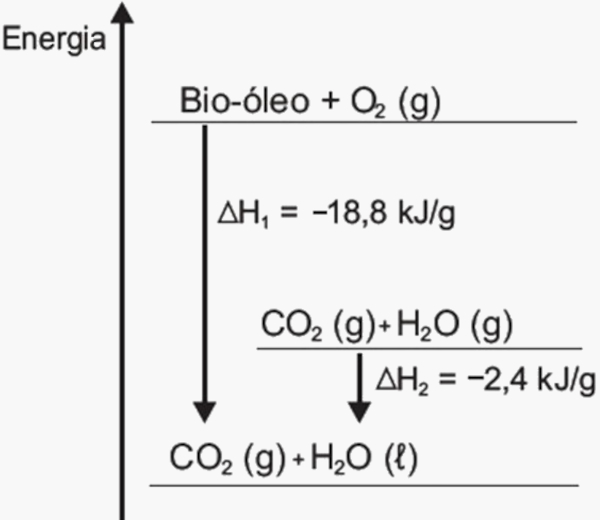
A lei de Hess é um mecanismo de cálculo da variação de entalpia de um processo químico por meio do somatório das entalpias de reação de etapas intermediárias do processo. Sendo a entalpia uma função de estado, não importa a quantidade de etapas realizadas no processo químico, pois, sendo o estágio inicial e o final os mesmos, a variação de entalpia também é a mesma.
A lei de Hess pode ser aplicada em processos químicos de difícil realização, por exigirem condições severas, como alta ou baixa pressão, alta ou baixa temperatura, ou que simplesmente não acontecem. Na metodologia da lei de Hess, as reações químicas podem ser operadas como equações em um sistema matemático. Ela foi desenvolvida pelo químico russo Germain Henry Hess no ano de 1840.
Leia também: O que é e como calcular a entalpia de uma reação
Tópicos deste artigo
- 1 - Resumo sobre a lei de Hess
- 2 - O que diz a lei de Hess?
- 3 - Aplicações da lei de Hess
- 4 - Como calcular a lei de Hess?
- 5 - O que é termoquímica?
- 6 - Diagrama de entalpia
- 7 - Quem foi Germain Henry Hess?
- 8 - Exercícios resolvidos sobre lei de Hess
Resumo sobre a lei de Hess
-
A lei de Hess é uma metodologia para cálculo da entalpia total de um processo químico que ocorre em mais de uma etapa reacional.
-
Segundo a lei de Hess, o somatório das entalpias de reação de todas as etapas é igual à entalpia total do processo químico.
-
Utiliza-se a lei de Hess para calcular a variação de entalpia de processos de difícil realização ou que não podem ser realizados em laboratório.
-
A lei de Hess é muito importante para a termoquímica, que é a área da termodinâmica que estuda o calor envolvido nas reações químicas.
-
A lei de Hess foi enunciada em 1840 pelo cientista russo Germain Henry Hess.
Anuncie aqui
O que diz a lei de Hess?
A lei de Hess é uma forma de calcular a entalpia total de uma reação química por meio da soma das entalpias de reação das diversas etapas em que essa reação química pode ser dividida.
A lei de Hess é uma consequência do fato de a entalpia (H) ser uma função de estado. Toda variação de uma função de estado depende apenas do estado inicial e final do sistema. Assim sendo, se uma reação química, com os mesmos reagentes e produtos, ocorrer por meio de duas etapas ou cinco etapas, a variação de entalpia será a mesma, pois essa variação depende apenas do estado inicial e do estado final da reação química.
Aplicações da lei de Hess
A lei de Hess é útil para determinar variações de entalpia de reações que não podem ser reproduzidas em laboratório. Por exemplo, o processo de sublimação é a passagem direta do estado sólido para o estado gasoso. Contudo, como a sublimação pode ser de difícil reprodução, podemos determinar sua entalpia desmembrando o processo em duas etapas: uma fusão e depois uma vaporização.
Como os estágios final (gás) e inicial (sólido) são os mesmos, seja pensando na sublimação, seja pensando na fusão e na vaporização posterior, podemos então dizer que a variação da entalpia de sublimação (∆Hsub) é igual ao somatório das variações de entalpia de fusão (∆Hfus) e vaporização (∆Hvap).
∆Hsub = ∆Hfus + ∆Hvap
Como calcular a lei de Hess?
Para calcular variações de entalpia por meio da lei de Hess, vamos pensar no processo de síntese do propano (C3H8) por meio de seus elementos no estado-padrão, algo difícil de ser feito em laboratório. Foque no fato de os reagentes serem o estado inicial e o produto, propano, ser o estado final.
3 C (graf.) + 4 H2 (g) → C3H8 (g)
Para calcular a entalpia da síntese do propano, vamos aproveitar as reações de combustão de cada participante, as quais são facilmente reprodutíveis em laboratório e de entalpia conhecida:
(a) C3H8 (g) + 5 O2 (g) → 3 CO2 (g) + 4 H2O (l) ∆H = –2220 kJ.mol–1
(b) C (graf.) + O2 (g) → CO2 (g) ∆H = –394 kJ.mol–1
(c) H2 (g) + ½ O2 (g) → H2O (l) ∆H = –286 kJ.mol–1
Com essas três reações, é possível criar um mecanismo (etapas) hipotético, que não necessariamente ocorre ou é a forma como essa reação se desenvolve. Salienta-se que o importante é que os estados inicial e final sejam os mesmos.
De modo prático, devemos somar as reações (a), (b) e (c) para atingir a reação de interesse. Mas essa soma ocorrerá de forma análoga a um sistema matemático, ou seja, é permitido inverter o sentido da reação química, bem como dividir ou multiplicar os coeficientes estequiométricos.
Observe a reação (a). Nela, o propano está como reagente. O nosso interesse é que o propano esteja como produto e, assim, é possível inverter o sentido da reação. Porém, ao fazermos isso, o sinal da variação de entalpia será invertido, afinal, se em um sentido a reação é exotérmica, no sentido inverso ela é endotérmica. Assim, a reação (a) fica:
(a) 3 CO2 (g) + 4 H2O (l) → C3H8 (g) + 5 O2 (g) ∆H = +2220 kJ.mol–1
Já ao avaliarmos a reação (b), notamos que o carbono na forma de grafite já é um reagente, porém é de nosso interesse que reajam 3 mols dele. Assim sendo, multiplicaremos toda a reação por 3 e, por consequência, o ∆H também será triplicado.
(b) 3 C (graf.) + 3 O2 (g) → 3 CO2 (g) ∆H = –1182 kJ
Continuando, são necessários 4 mols de H2 como reagente. A reação (c) já coloca o gás hidrogênio como reagente, mas há apenas 1 mol dele. Dessa forma, semelhantemente ao que fizemos na reação (b), iremos multiplicar a reação (c) por 4.
(c) 4 H2 (g) + 2 O2 (g) → 4 H2O (l) ∆H = –1144 kJ
Caso as análises e alterações tenham sido corretas, ao somar (a), (b) e (c), obteremos a reação de interesse. Ao somar, substâncias iguais em lados opostos devem ser subtraídas, como é possível ver a seguir:
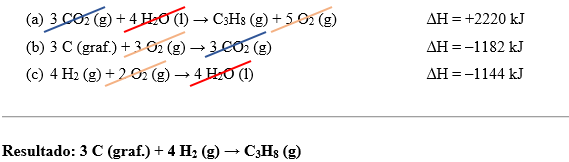
Como o resultado obtido corresponde à reação de interesse, o ∆H da reação obtida será simplesmente o somatório dos valores de variação de entalpia das três reações utilizadas:
∆H = 2220 – 1182 – 1144
∆H = –106 kJ
Leia também: Energia Livre de Gibbs — energia para realizar trabalho útil em temperatura e pressão constantes
O que é termoquímica?
A termoquímica é o estudo da demanda de calor pelas reações químicas, ou seja, estuda quanto de energia é transferida na forma de calor durante os processos químicos.
A termoquímica é um ramo da termodinâmica, pois utiliza as suas leis e princípios. Por exemplo, uma reação química que ocorre em um frasco em uma bancada de laboratório ou em um reator na indústria é um sistema. Ao longo do desenrolar das reações químicas, energia é trocada com a vizinhança desse sistema. Se a energia trocada com a vizinhança ocorrer na forma de calor, é possível utilizar a calorimetria para mensurar quanto de energia foi fornecida ou liberada na forma de calor. Contudo, o calor envolvido em uma reação química é avaliado pela variação de entalpia (∆H), pois, em pressão constante, a variação da energia trocada na forma de calor é numericamente igual à variação de entalpia.
Diagrama de entalpia
A lei de Hess também pode ser aplicada nos diagramas do Ciclo de Born-Haber, como mostra a imagem a seguir.
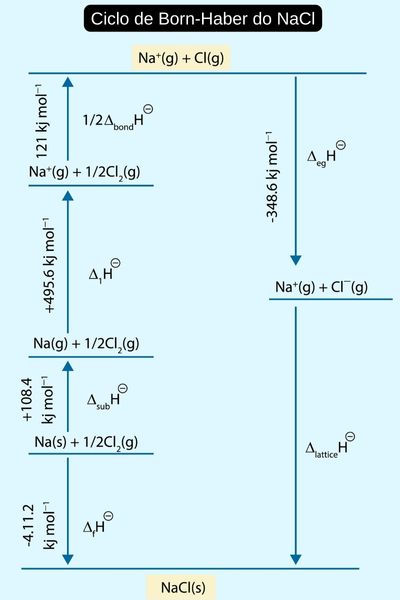
Assim sendo, o ∆H do processo total é dado pela seguinte expressão:
∆H = + 411,2 kJ + 108,4 kJ + 495,6 kJ + 121 kJ = 1136,2 kJ
Essa expressão é basicamente a soma das distâncias energéticas dadas pelo diagrama.
Com o valor do ∆H do processo global, é possível determinar a entalpia de rede do NaCl (∆Hlattice) pelo diagrama. Repare que, com a seta apontando para baixo (em direção ao NaCl), essa entalpia de rede é exotérmica (∆H < 0) e, portanto, terá um valor negativo.
Agora o nosso ponto de partida não é mais o NaCl (s), mas os produtos da reação anterior. Então, a reação para determinar a entalpia de rede será:
Na+ (g) + Cl (g) → NaCl (s)
E, por isso, o ∆H é invertido, ficando exotérmico e igual a –1136,2 kJ.
Para calcular a entalpia de rede pelo diagrama, faz-se:
–1136,2 = –348,6 + ∆Hlattice
∆Hlattice = –787,6 kJ
Quem foi Germain Henry Hess?
Germain Henry (às vezes grifado como Henri) Hess foi um químico russo que viveu entre os anos de 1802 e 1850. Depois de estudar medicina, Hess se tornou professor de química, em 1830, no Instituto Tecnológico de São Petersburgo.
Sua lei foi anunciada em 1840, na qual dizia que o calor envolvido em uma reação química seria sempre o mesmo, independentemente da quantidade de etapas que fossem realizadas. A lei é focada na ideia da conservação de energia e serviu como base para que fosse desenvolvida a termoquímica no final do século XIX pelo físico americano Josiah Willard Gibbs.
Exercícios resolvidos sobre lei de Hess
Questão 1
(Mackenzie/2022) De acordo com a Lei de Hess, “A variação de entalpia (ΔH) em uma reação química depende apenas dos estados inicial e final da reação, independentemente do número de reações.” Desse modo, a partir das equações termoquímicas fornecidas abaixo e aplicando os princípios dessa lei, o valor da entalpia-padrão de combustão do etanol, é da ordem de:
C(graf) + O2 (g) → CO2 (g) ΔH0f = − 394 kJ·mol-1.
H2 (g) + ½ O2 (g) → H2O (l) ΔH0f = − 286 kJ·mol-1.
2 C(graf) + 3 H2 (g) + ½ O2 (g) → C2H6O (l) ΔH0f = − 278 kJ·mol-1.
(A) − 228 kJ·mol-1.
(B) − 342 kJ·mol-1.
(C) − 684 kJ·mol-1.
(D) − 1368 kJ·mol-1.
(E) − 2736 kJ·mol-1.
Resposta: Letra D.
A combustão de 1 mol etanol é dada pela seguinte reação química:
C2H6O (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l)
Dessa forma, deve-se utilizar as equações fornecidas para criar um mecanismo/rota reacional até a combustão do etanol. Assim sendo, pensando-se na primeira reação, vê-se que o CO2 (g) já está do lado dos produtos, porém na quantidade errada. Por isso, multiplica-se a primeira equação por 2.
2 C(graf) + 2 O2 (g) → 2 CO2 (g) ΔH = − 788 kJ
Na segunda equação química, a água também se apresenta como produto, mas, assim como o dióxido de carbono, está na quantidade indevida. Por isso, multiplica-se a segunda equação por 3.
3 H2 (g) + 3/2 O2 (g) → 3 H2O (l) ΔH = − 858 kJ
Por fim, a última equação possui o etanol na quantidade correta, mas como produto. Como na combustão ele se apresenta como um reagente, inverteremos a última equação:
C2H6O (l) → 2 C(graf) + 3 H2 (g) + ½ O2 (g) ΔH = + 278 kJ
Agora iremos somar as três reações. Caso tenhamos feito os ajustes adequados, chegaremos à reação de combustão do etanol e assim validaremos a nossa rota reacional proposta:
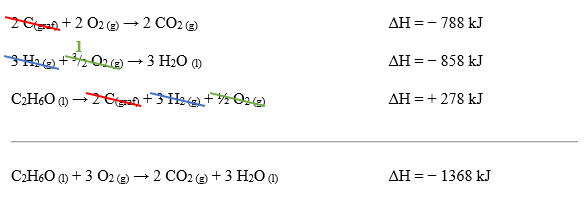
Questão 2
(PUC-MG/2021) A Lei de Hess diz que a variação de entalpia envolvida em uma reação química, sob certas condições experimentais, depende exclusivamente da entalpia inicial e final dos produtos, seja a reação executada diretamente em uma única etapa ou indiretamente, em uma série de etapas.
Considere o gráfico a seguir:
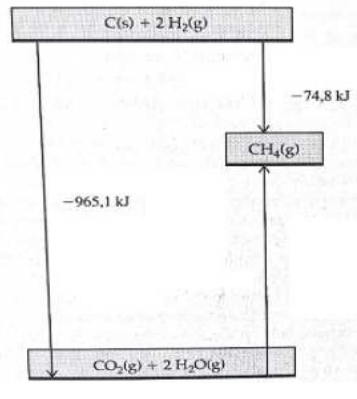
A energia envolvida na formação do gás metano a partir de gás carbônico e água é:
(A) – 1039,9 kJ
(B) – 890,3 kJ
(C) + 1039,9 kJ
(D) + 890,3 kJ
Resposta: Letra D.
A formação do gás metano a partir de gás carbônico e água é a única seta do diagrama que não apresenta valor de variação de entalpia. A distância energética pode ser feita da seguinte forma:
965,1 = 74,8 + ∆H
Repare que os valores estão sendo postos em módulo, o sinal será decidido depois.
Ao fazer essa conta, tem-se que:
∆H = 965,1 – 74,8
∆H = 890,3
Sendo a seta sentido ascendente, diferentemente das outras duas setas presentes no diagrama, pode-se dizer então que o valor para o ∆H é positivo, caracterizando o processo como endotérmico. Por isso, o ∆H = + 890,3 kJ para a formação do gás metano a partir de gás carbônico e água.
Fontes
DO CANTO, E. L.; LEITE, L. L. C.; CANTO, L. C. Química – na abordagem do cotidiano. 1. ed. São Paulo: Moderna, 2021.
ATKINS, P.; JONES, L.; LAVERMAN, L. Princípios de Química: Questionando a vida e o meio ambiente. 7. ed. Porto Alegre: Bookman, 2018.
ATKINS, P.; DE PAULA, J.; KEELER, J. Atkins’s Physical Chemistry. 11 ed. Oxford: Oxford University Press, 2018.
BRITANNICA. Germain Henri Hess. Britannica. 03 ago. 2023. Disponível em: < https://www.britannica.com/biography/Germain-Henri-Hess>.