Equações Termoquímicas

As equações químicas são formas de se representar as reações químicas. De modo similar, as equações termoquímicas são usadas para representar os processos que envolvem troca de calor, que podem ser endotérmicos (com absorção de calor) ou exotérmicos (com liberação de calor).

Nessas equações aparecem os mesmos símbolos (como as fórmulas e os estados físicos das substâncias) e números (como índices e coeficientes) que aparecem em uma equação química normal. Se desejar, poderá consultar os artigos abaixo para tirar quaisquer dúvidas acerca desses termos qualitativos e quantitativos das equações químicas:

* Equação química;

* Termos quantitativos de uma equação química.

Assim, nas equações termoquímicas, é muito importante indicar todos os fatores que podem interferir no valor da entalpia (H), ou seja, no conteúdo de energia das substâncias. Entre esses dados importantes que devem ser citados e que também aparecem nas equações químicas comuns, estão:

* A proporção estequiométrica entre os reagentes e os produtos, que são dados pelos coeficientes devidamente balanceados, isto é, o número de mol dos elementos participantes;

* Os estados físicos das espécies químicas (fórmulas, moléculas, íons, átomos, etc.), por meio do símbolo que aparece no canto inferior direito. Por exemplo: água no estado líquido: H₂O_(ℓ);

* Estrutura cristalina ou alotrópica (se for o caso). Por exemplo: S_(rômbico).

Mas nas equações termoquímicas aparecem também outros dois dados que as diferenciam das equações comuns, que são:

* A temperatura e a pressão em que o processo ocorre. Se essas informações não estiverem escritas na equação, consideram-se as condições ambientes em que a temperatura é dada em 298 K ou 25 ºC e a pressão é dada por 1 atm.

Essas condições são as indicadas porque as entalpias sempre são avaliadas em relação a uma mesma condição, isto é, uma condição ou estado padrão, em que a substância está na sua forma alotrópica mais estável, a 1 atm e 25 ºC. Essa entalpia padrão é indicada por H⁰.

* Variação da entalpia (∆H): Esse é o aspecto mais importante das equações termoquímicas, pois é ele que identifica a quantidade de energia que foi perdida ou ganhada na forma de calor e se o processo é endotérmico ou exotérmico, sendo que:

- ∆H < 0 (variação da entalpia negativa): processo exotérmico.

Se o valor da variação do calor envolvido na reação for negativo, isso indica que a substância liberou calor, porque ∆H = H_final - H_inicial ou ∆H = H_produtos - H_reagentes. Visto que o valor da entalpia dos produtos é menor que o dos reagentes, então o valor de ∆H será realmente menor que zero.

Portanto, uma forma alternativa de se identificar esse tipo de reação é pela seguinte notação:

Reagentes → Produtos + Energia

- ∆H > 0 (variação da entalpia positiva): processo endotérmico.

O valor positivo para ∆H indica que a entalpia dos produtos é maior que a dos reagentes, o que significa que houve absorção de calor. Assim, as reações podem ser identificadas pela notação a seguir:

Reagentes + Energia → Produtos + Energia

Temos, então, que a notação genérica de uma equação termoquímica é dada por:

Reagentes → Produtos ∆H = Energia (em kJ/mol)

Vejamos alguns exemplos de como escrever as equações termoquímicas de algumas reações que envolvem troca de calor.

Exemplo 1: A combustão completa do gás metano (CH_4(g)) produz dióxido de carbono e água, liberando 890,4 kJ de energia por mol de metano que reage. A equação termoquímica que representa essa reação de combustão é dada por:

1 CH_4(g) + 2 O_2(g) →1 CO_2(g) + H₂O_(ℓ) ∆H = - 890,4 kJ/mol

Exemplo 2: A formação de 1 mol de hematita (minério do ferro – Fe₂O_3(s)) em ferro metálico (Fe_(s)) ocorre com absorção de 490 kJ. Sua equação termoquímica é:

Fe₂O_3(s) +3 C_(s) → 2 Fe_(s) +3 CO_(g) ∆H = + 490 kJ/mol

Exemplo 3: Observe as seguintes equações comuns abaixo e veja logo abaixo de cada uma como ficam as suas respectivas equações termoquímicas:

I. 6 CO_2(g) + 6 H₂O_(ℓ) + 2 813 → C₆H₁₂O_6(g) + 6 O_2(g)

Equação termoquímica: 6 CO_2(g) + 6 H₂O_(ℓ) → C₆H₁₂O_6(g) + 6 O_2(g) ∆H = + 2 813 kJ/mol

II. HCℓ_(aq) + NaOH_(aq) → NaCℓ_(aq) + H₂O_(ℓ) + 57,7

Equação termoquímica:HCℓ_(aq) + NaOH_(aq) → NaCℓ_(aq) + H₂O_(ℓ) ∆H = - 57,7 kJ

As equações termoquímicas não são usadas para representar somente reações químicas, mas também processos físicos em que há trocas de calor, como as mudanças de estados físicos. Veja abaixo as mudanças de estado físico da água e as equações termoquímicas em cada caso:

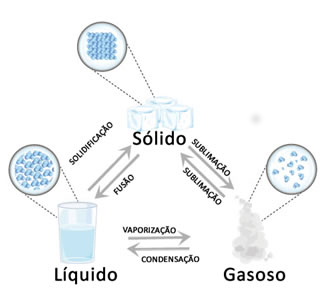
Fusão: H₂O_(s) → H₂O_(ℓ) ∆H = + 7,3 kJ

Solidificação: H₂O_(ℓ) → H₂O_(s) ∆H = - 7,3 kJ

Vaporização: H₂O_(ℓ) → H₂O_(v) ∆H = + 44 kJ

Condensação: H₂O_(v) → H₂O_(ℓ) ∆H = - 44 kJ

Observe que quando um processo é inverso ao outro, o valor da variação de entalpia é o mesmo, porém, com sinais opostos, pois em um processo está ocorrendo absorção de calor (endotérmico), enquanto no outro está ocorrendo liberação de calor (exotérmico).

Dessa forma, nunca esqueça: se for inverter uma equação termoquímica, lembre-se de inverter também o sinal de ∆H.

Outro aspecto importante que precisamos mencionar é que quando uma reação química ocorre em várias etapas e são representadas várias equações, a soma de todas elas (equação global) envolve também a soma dos valores de ∆H:

Veja um exemplo:

(Fuvest-SP) O “besouro bombardeiro” espanta seus predadores, expelindo uma solução quente. Quando ameaçado, em seu organismo ocorre a mistura de soluções aquosas de hidroquinona, peróxido de hidrogênio e enzimas, que promovem uma reação exotérmica representada por:

C₆H₄(OH)_2(aq) + H₂O_2(aq) → C₆H₄O_2(aq) + 2 H₂O_(l)
O calor envolvido nessa transformação pode ser calculado, considerando-se os processos:

C₆H₄(OH)_2(aq) → C₆H₄O_2(aq) + H_2(g) ∆H = +177 kJ/mol
H₂O_(l) + 1/2 O_2(g) → H₂O_2(aq) ∆H = +95 kJ/mol
H₂O_(l) → 1/2 O_2(g) + H_2(g) ∆H = +286 kJ/mol
Assim sendo, o calor envolvido na reação que ocorre no organismo do besouro é:

a) -558 kJ . mol^-1.

b) -204 kJ . mol^-1.

c) +177 kJ . mol^-1.

d) +558 kJ . mol^-1.

e) +585 kJ . mol^-1.

Resolução:

Pela Lei de Hess, encontramos o valor de ∆H da reação pela álgebra dos valores de ∆H do primeiro processo com os do segundo e do terceiro invertidos:

C₆H₄(OH)_2(aq) → C₆H₄O_2(aq) + H_2(g) ∆H = +177 kJ/mol

H₂O_2(aq) → H₂O_(l) + 1/2 O_2(g) ∆H = -95 kJ/mol

1/2 O_2(g) + H_2(g)→ H₂O_(l) ∆H = - 286 kJ/mol

C₆H₄(OH)_2(aq) + H₂O_2(aq) → C₆H₄O_2(aq) + 2 H₂O_(l) ∆H = +177 + (-95) + (-286) →∆H = -204 kJ/mol

Alternativa “b”.

Por Jennifer Fogaça
Graduada em Química