Ângulo entre dois vetores

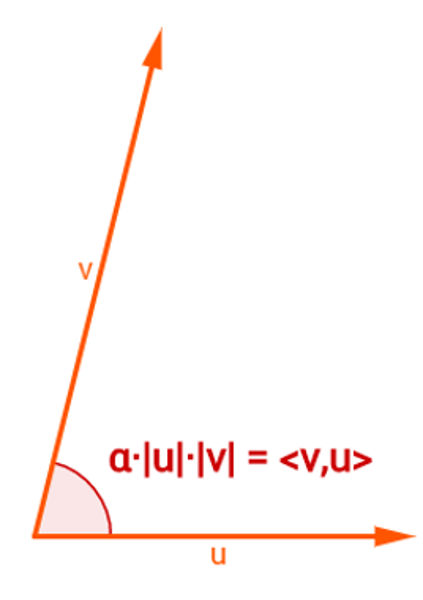
Vetores são objetos matemáticos responsáveis por descrever a trajetória de pontos. Por muitas vezes, esses pontos representam objetos concretos em movimento, o que é estudado minuciosamente pela Física. Ao considerar as forças envolvidas na movimentação (de fato ou em potencial) de um objeto, a Física faz uso dos vetores para representá-las. O ângulo que esses vetores formam é parte crucial nos cálculos, pois uma pequena variação no ângulo pode exigir que mais força seja aplicada sobre um objeto para que ele inicie ou permaneça em movimento.

Os vetores são representados geometricamente por flechas, que são segmentos de reta orientados. Assim, uma das extremidades do segmento indica a posição final do ponto movimentado, e a outra extremidade não recebe marcação, indicando que foi ali que o movimento teve início. O ponto de localização da extremidade final, geralmente, é utilizado para identificar um vetor que se inicia na origem de um sistema de coordenadas. Considerando o plano cartesiano como sistema de coordenadas, um vetor v, que se inicia no ponto (0,0) e finda no ponto (a,b), é representado apenas como vetor v = (a,b). Se o vetor se iniciar em outro ponto, basta movimentá-lo para o local apropriado.

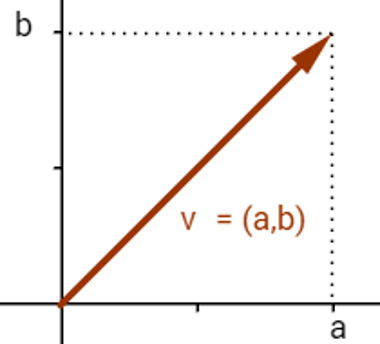
Vetor no plano cartesiano

Como se trata de segmentos de reta orientados, é possível calcular seu comprimento, que é chamado de norma do vetor. O cálculo da norma de um vetor é dado da mesma maneira que a distância entre dois pontos e é equivalente ao cálculo do módulo de um número real. Dessa maneira, a norma do vetor v = (a,b) é denotada por |v| e pode ser calculada da seguinte maneira:

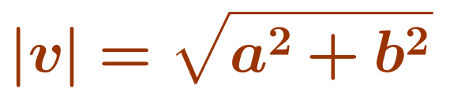
Considerando dois vetores v = (a,b) e u = (a',b'), o produto interno entre eles é denotado por <v,u> e é dado pela seguinte expressão:

<v,u> = a·a' + b·b'

O produto interno entre dois vetores também é definido por meio do ângulo entre eles. Essa definição torna possível o cálculo do ângulo entre dois vetores.

Ângulo entre dois vetores

Dessa maneira, tomando os mesmos vetores v e u, o cosseno do ângulo θ entre eles é dado pela seguinte expressão:

cosθ = <v,u>
           |v|·|u|

De posse desses dados, definições e, de certa maneira, fórmulas, é possível traçar uma estratégia para calcular o ângulo entre dois vetores.

Dados os vetores v = (2,2) e u = (0,2), calcularemos o ângulo entre eles. Para tanto, primeiramente, calcule a norma de cada vetor e o produto entre essas normas:

|v| = √(2² + 2²)
|v| = √(4 + 4)
|v| = √8

|u| = √(0² + 2²)
|u| = √(0 + 4)
|u| = √4

|v|·|u| = √8·√4
|v|·|u| = 4√2

Posteriormente, calcule o produto interno entre v e u:

<v,u> = 2·0 + 2·2
<v,u> = 0 + 4
<v,u> = 4

Por fim, utilize a fórmula do ângulo entre vetores para calcular o cosθ e a tabela de valores dos cossenos para encontrar o valor de θ.

cosθ = <v,u>
           |v|·|u|

cosθ =    4   
           4√2

cosθ =    4   
            4√2

cosθ =    2   
          √2

cosθ = √2
           2

θ = 45°

Por Luiz Paulo Moreira
Graduado em Matemática