Operações com vetores e representações geométricas

Diferentemente das figuras geométricas formadas por ele, o ponto não possui definição. Isso significa que, em Geometria, ponto é um objeto não definido usado na definição de outros objetos. As retas, por exemplo, são conjuntos de pontos. Apesar de parecerem bem definidas, as retas também não possuem definição, pois, qualquer conjunto contendo dois ou mais pontos é considerado reta.

Por outro lado, na Geometria Analítica, o ponto é tido como uma localização. Qualquer local pode ser representado por um ponto e, além disso, o “endereço” desse ponto é dado por meio de coordenadas.

Entretanto, na Geometria Analítica, os pontos são capazes apenas de indicar localizações. Outros objetos são necessários para indicar trajetória, direção, sentido e intensidade. No caso desses últimos três, o objeto escolhido para representá-los no plano cartesiano é o vetor.

→ O que é um Vetor?

Vetores, portanto, são objetos que indicam direção, sentido e intensidade. São usualmente representados por setas, que partem da origem, e utilizam-se as coordenadas de seu último ponto.

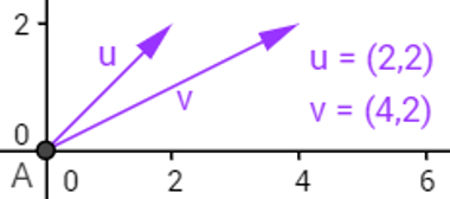
Na imagem acima, os vetores são representados dessa forma, isto é, setas cujas coordenadas correspondem ao seu ponto final. O vetor u possui coordenadas (2,2) e o vetor v possui coordenadas (4,2). Além disso, a seta é utilizada para indicar direção e sentido, e o seu tamanho indica a intensidade.

→ Multiplicação de vetor por um número

Dado o vetor v = (a,b), o produto do número real k por v é dado pela expressão:

k·v = k·(a,b) = (k·a, k·b)

Em outras palavras, para multiplicar um número real por um vetor, deve-se multiplicar o número real por cada uma de suas coordenadas.

Geometricamente, a multiplicação de um vetor por um número real aumenta o tamanho do vetor linearmente:

Note que, no exemplo acima, o vetor u possui coordenadas (2,2), e o vetor u·k possui coordenadas (4,4). Resolvendo a equação (4,4) = k(2,2), pode-se concluir que k = 2.

→ Adição de vetores

Dados dois vetores u = (a,b) e v = (c,d), a soma entre eles será obtida por meio da expressão:

u + v = (a + c, b + d)

Em outras palavras, basta somar as coordenadas correspondentes de cada vetor. Essa operação é expansível para soma de 3 ou mais vetores com 3 ou mais dimensões.

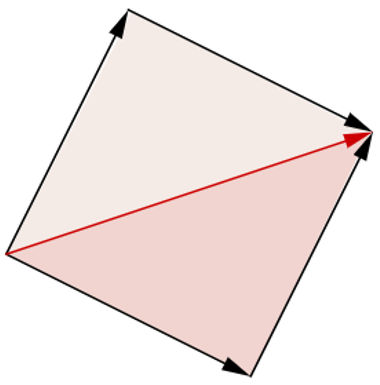
Geometricamente, partindo do ponto final do vetor u, desenha-se um vetor v' paralelo ao vetor v. Partindo do vetor v, desenha-se um vetor u' paralelo ao vetor u. Esses quatro vetores formam um paralelogramo. O vetor u + v é a seguinte diagonal desse paralelogramo:

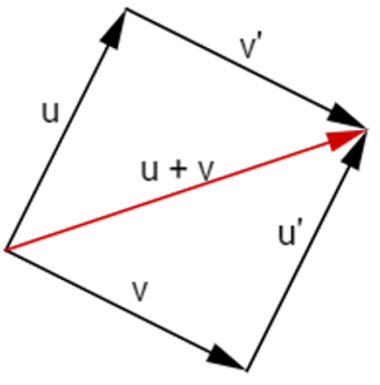
Para subtrair vetores, considere subtração como soma entre um vetor e o oposto de outro. Por exemplo, para subtrair o vetor v do vetor u, escreve-se: u – v = u + (-v). O vetor -v é o vetor v, porém, com os sinais das coordenadas invertidos.

Observando atentamente, as operações “multiplicação de um vetor por um número” e “adição de vetores” fazem o uso das operações de multiplicação e adição nos números reais, mas em cada componente do vetor. Portanto, para os vetores, são válidas todas as propriedades de soma e multiplicação de números reais, a saber:

Dados os vetores u, v e w e os números reais k e l,

i) (u + v) + w = u + (v + w)

ii) u + v = v + u

iii) existe um vetor 0 = (0,0) tal que v + 0 = v

iv) Existe um vetor -v tal que v + (-v) = 0

v) k(u + v) = ku + kv

vi) (k + l)v = kv + lv

vii) kl(v) = k(lv)

viii) 1v = v

→ Norma de um vetor

A norma de um vetor é o equivalente ao módulo de um número real, ou seja, a distância entre um vetor e o ponto (0,0) ou, dependendo do referencial, o comprimento do vetor.

A norma do vetor v = (a,b) é denotada por ||v|| e pode ser calculada por meio da expressão:

||v|| = √(a² + b²)

→ Produto interno

Produto interno é comparável ao produto entre vetores. Note que o produto já citado anteriormente é o produto entre um vetor e um número real. Agora, o “produto” em questão é entre dois vetores. Contudo, não se deve dizer “produto entre dois vetores”, mas, sim, “produto interno entre dois vetores”. O produto interno entre os vetores v = (a,b) e u = (c,d) é denotado por <v,u> e pode ser calculado da seguinte maneira:

<v,u> = a·c + b·d

Também é costume utilizar a seguinte notação:

<v,u> = <(a,b),(c,d)>

Observe que, utilizando a norma do vetor v = (a,b), podemos relacionar norma e produto interno.

||v|| = √(a² + b²) = √(a·a + b·b) = √(<v,v>)

Por Luiz Paulo Moreira
Graduado em Matemática