Produto interno entre dois vetores

O produto interno entre dois vetores é um número real que relaciona o módulo desses vetores, isto é, seu comprimento, e o ângulo entre eles. Para calculá-lo, é necessário, portanto, conhecer seus comprimentos e o ângulo que eles formam.

Utilizando o plano como base, um vetor indica uma localização, uma intensidade, uma direção e um sentido. Por isso, é utilizado nos estudos da Mecânica (Física) como representante de uma força aplicada a um objeto.

A representação usual do vetor é uma flecha que finda em um ponto. Diz-se que as coordenadas desse ponto são as coordenadas do vetor que parte do ponto O (0,0). Escrevemos v = (a,b) para representá-lo. Dessa forma, o vetor v = (1,2) é desenhado da seguinte maneira:

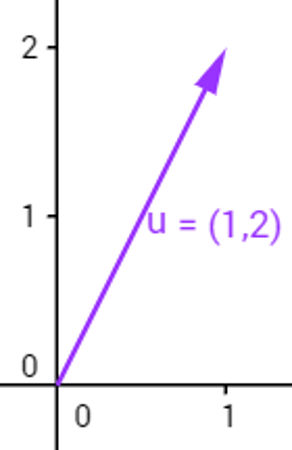
Exemplo de vetor partindo da origem

Para calcular o comprimento desse vetor, considera-se o triângulo retângulo formado por ele e sua projeção no eixo x (ou no eixo y), conforme a figura a seguir:

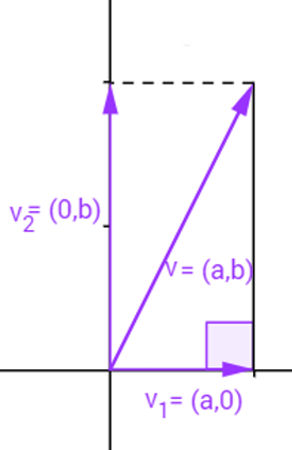
Comprimento do vetor v

O comprimento de um vetor v é chamado de norma do vetor v ou módulo do vetor v e é representado por |v|. Observe que a norma do vetor v = (a,b) é justamente a medida da hipotenusa do triângulo representado na figura acima. Para calcular essa medida, utilizamos o Teorema de Pitágoras:

|v|² = a² + b²

|v| = √(a² + b² )

Produto interno de dois vetores

Dados dois vetores u e v, o produto interno entre eles é representado por <u,v> e é definido como:

<u,v> = |u||v|·cosθ

Essa é uma espécie de multiplicação entre dois vetores, porém, não recebe o nome de produto por não ser uma multiplicação comum, uma vez que envolve o ângulo formado por esses dois vetores.

Ângulo entre dois vetores

O primeiro resultado decorrente da definição acima é o ângulo entre dois vetores. De posse dos números reais “produto interno”, “norma do vetor u” e “norma do vetor v”, é possível calcular o ângulo entre os vetores u e v. Para isso, basta realizar os cálculos:

<u,v> = |u||v|·cosθ

<u,v> = cosθ
|u||v|           

Portanto, dividindo o produto interno pelas normas dos vetores u e v, encontramos o número real referente ao cosseno entre esses dois vetores e, portanto, o ângulo entre eles.

Observe que, caso o ângulo entre dois vetores seja reto, o cosθ será igual a zero. Logo, o produto acima terá o seguinte resultado:

<u,v> = 0

A partir disso, pode-se concluir que, dados dois vetores u e v, eles serão ortogonais se <u,v> = 0.

Produto interno calculado a partir das coordenadas dos vetores

Considerando os dois vetores u = (a,b) e v = (c,d), o produto interno entre u e v é dado por:

<u,v> = <(a,b),(c,d)> = a·c + b·d

Propriedades do produto interno

Dados os vetores u, v e w e o número real α, observe:

i) <u,v> = <v,u>

Isso significa que o produto interno de vetores é “comutativo”.

ii) <u + v, w> = <u,w> + <v,w>

Essa propriedade é comparável à distributividade da multiplicação sobre a adição.

iii) <αu,v> = <u,αv> = α<u,v>

Calcular o produto interno entre u e v multiplicado pelo número real α é o mesmo que calcular o produto interno entre αv e u ou entre v e αu.

iv) <v,v> = 0 <=> v = 0

O produto interno de v com v só será zero se v for o vetor nulo.

v) <v,v> ≥ 0 para todo v.

O produto interno de v com v sempre será maior ou igual a zero.

Por Luiz Paulo Moreira
Graduado em Matemática