Probabilidade condicional

Conhecemos como probabilidade condicional a probabilidade de um determinado evento ocorrer, sabendo que um evento condicionante já aconteceu. Dados dois eventos A e B, inicialmente com o mesmo espaço amostral, a probabilidade condicional é representada por P(A|B) e significa a probabilidade do evento A ocorrer, dado que o evento B ocorreu. Existe uma fórmula específica que ajuda a resolver problemas de probabilidade condicional.

Leia também: Os três erros mais cometidos no cálculo de probabilidade

Tópicos deste artigo

• 1 - Resumo sobre a probabilidade condicional
• 2 - Videoaula sobre probabilidade condicional
• 3 - Espaço amostral
• 4 - Evento
• 5 - O que é probabilidade condicional?
• 6 - Fórmula para calcular a probabilidade condicional
• 7 - Como se calcula a probabilidade condicional?
• 8 - Exercícios resolvidos sobre probabilidade condicional

Resumo sobre a probabilidade condicional

• A probabilidade condicional é a chance de o evento A acontecer, dado que B já aconteceu.

• O evento B é conhecido como condicionante, então, calculamos a chance de o evento A acontecer na condição de o evento B ter acontecido.

• Existem duas fórmulas para calcular a probabilidade condicional.

→ A primeira fórmula da probabilidade condicional é:

→ Podemos calcular a probabilidade condicional também pela fórmula:

Videoaula sobre probabilidade condicional

Espaço amostral

Para compreender o que é a probabilidade condicional, é importante relembrar o que é o espaço amostral. Em um experimento aleatório, conhecemos como espaço amostral o conjunto com todos os resultados possíveis para esse experimento.

Exemplo 1:

Quando lançamos um dado comum e observamos o resultado da face superior, nosso espaço amostral são os números {1, 2, 3, 4, 5, 6}. O espaço amostral é normalmente representado pelo símbolo Ω (lê-se: ômega), ou seja, nesse caso, Ω = {1, 2, 3, 4, 5, 6}.

Exemplo 2:

Ao realizar o lançamento de uma moeda comum três vezes consecutivas, teremos o seguinte espaço amostral:

Ω = {(cara, cara, cara); (cara, cara, coroa); (cara, coroa, cara); (coroa, cara, cara); (coroa, coroa, cara); (coroa, cara, coroa); (cara, coroa, coroa); (coroa, coroa, coroa)}

Evento

Conhecemos como evento um determinado conjunto de resultados que queremos que ocorra no experimento aleatório, o evento é sempre um subconjunto do espaço amostral.

Exemplo 1:

Ao lançar o dado, queremos que o resultado seja um número primo.

Então, nesse caso, o evento é sair um número primo, e os resultados favoráveis são A = {2, 3, 5}.

Exemplo 2:

Ao lançar o dado, queremos que o resultado seja um número par.

Então, nesse caso, o evento é sair um número par e os resultados favoráveis são B = {2, 4, 6}.

Exemplo 3:

No lançamento da moeda por três vezes sucessivas, queremos que o resultado seja sair cara somente uma vez. Nesse evento, os casos favoráveis são C = {(cara, coroa, coroa); (coroa, cara, coroa); (coroa, coroa, cara)}.

Veja também: O que é o princípio fundamental da contagem?

O que é probabilidade condicional?

A probabilidade condicional é a chance de um determinado evento acontecer tendo como base que um evento aconteceu anteriormente; ambos os eventos possuem o mesmo espaço amostral. Esse evento que ocorreu anteriormente é conhecido como condicionante.

Dizemos que a probabilidade de o evento A acontecer, sabendo que o evento B aconteceu, é conhecida como probabilidade condicional do evento A dado B, representada por P(A|B) (lê-se: probabilidade de A dado B). Essa probabilidade só existe se os eventos possuírem o mesmo espaço amostral (diferente do vazio) e se B não for um evento impossível.

Exemplo 1:

Durante o lançamento de dois dados, queremos calcular a probabilidade de o resultado da soma das faces superiores ser igual a 6, sabendo que o resultado do lançamento dos dados são dois números pares.

Perceba que há dois eventos:

B → As duas faces são números pares.

A → A soma das faces superiores é igual a 6.

Então, queremos a probabilidade P(A|B): P(A soma das faces superiores é 6 | As duas faces são números pares).

Exemplo 2:

Em um conjunto de pessoas, entre homens e mulheres, uma delas será sorteada aleatoriamente. Uma possível probabilidade condicional é a probabilidade de a pessoa sorteada usar óculos, sabendo que o sorteado foi um homem.

B → O sorteado é um homem.

A → O sorteado usa óculos.

P(A|B) = P(O sorteado usa óculos | O sorteado é um homem)

Agora que conhecemos as situações que envolvem a probabilidade, veremos a fórmula utilizada para calcular a probabilidade condicional.

Fórmula para calcular a probabilidade condicional

Para calcular a probabilidade P(A|B), utilizamos a fórmula:

Analisando a fórmula, é possível simplificá-la para calcular a probabilidade condicional:

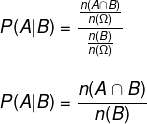
Como se calcula a probabilidade condicional?

Para calcular a probabilidade condicional, podemos utilizar qualquer uma das fórmulas supracitadas.

Exemplo:

Uma moeda comum foi lançada três vezes e o resultado foi anotado. Qual é a probabilidade de se obter exatamente duas caras sabendo que o primeiro resultado foi cara?

Primeiro identificamos o evento B, lembrando que ele é condicionante.

B → O primeiro lançamento é cara.

B = {(cara, coroa, coroa); (cara, cara coroa); (cara, coroa cara); (cara, cara, cara)}

n(B) = 4

Agora identificaremos o evento A∩B:

A → O resultado possui exatamente duas caras.

A∩B → O resultado possui exatamente duas caras, e o primeiro resultado é cara.

{(cara, cara coroa); (cara, coroa cara)}

n(A∩B) = 2

Então, P(A|B) pode ser calculado por:

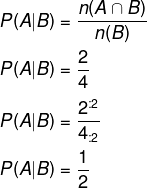
Exercícios resolvidos sobre probabilidade condicional

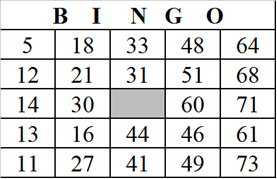
Questão 1 - (Enem) O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5, e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:

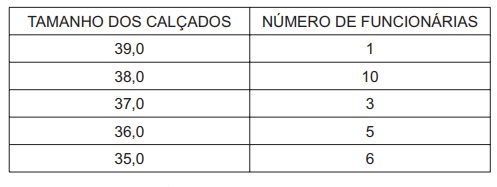
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0, a probabilidade de ela calçar 38,0 é:

A) 1/3

B) 1/5

C) 2/5

D) 5/7

E) 5/14

Resolução

Alternativa D

Note que esse problema envolve uma probabilidade condicional. Queremos calcular a probabilidade de a funcionária escolhida calçar 38,0 dado que ela calça mais que 36.

B → Calçar mais que 36

A → Calçar 38

A∩B → A intersecção é o conjunto formado pelas pessoas que calçam mais que 36 e que calçam 38, logo, ele é formado exclusivamente pelas 10 funcionárias que calçam 38.

n(B) = 3 + 10 + 1 = 14

n(A∩B) = 10

Então, temos que:

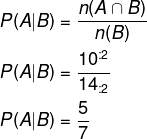
Questão 2 - Em uma sala de aula, o professor construiu a tabela a seguir com as características dos seus alunos:

Se um estudante for sorteado ao acaso, qual é a probabilidade de ele ser um homem sabendo que esse estudante não usa óculos?

A) 4%
B) 10%
C) 15%
D) 40%
E) 60%

Resolução

Alternativa D

Os eventos são:

B → O sorteado usa óculos.

A → O sorteado é um homem.

A∩B → O sorteado usa óculos e é um homem.

Sabemos que o sorteado usa óculos, então: n(B) = 10 + 15 = 25.

Também temos que n(A∩B) = 10

Dessa forma, podemos calcular a probabilidade condicional:

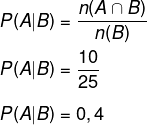
Sabemos que 0,4 = 40%.

Por Raul Rodrigues de Oliveira
Professor de Matemática