Probabilidade da união de dois eventos

A probabilidade da união de dois eventos é a probabilidade de um primeiro ou de um segundo evento ocorrer. No âmbito da probabilidade, estudamos a chance de determinados eventos ocorrerem, e em alguns casos é necessário calcular a probabilidade da união de dois eventos. Por exemplo, a probabilidade de um número sorteado ser ímpar ou primo.

Dados dois eventos, A e B, em um mesmo espaço amostral, para calcular a probabilidade da união de dois eventos, utilizamos a fórmula:

P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

Portanto, a probabilidade da união de dois eventos é igual à soma da probabilidade de cada um desses eventos ocorrerem menos a intersecção entre esses os dois. Quando os eventos são mutuamente excludentes, ou seja, a intersecção entre eles é vazia, então a probabilidade da união é a soma das probabilidades de ocorrência de cada um deles.

Leia também: Os três erros mais cometidos no cálculo de probabilidade

Tópicos deste artigo

• 1 - Resumo da probabilidade da união de dois eventos
• 2 - Qual a fórmula da probabilidade da união de dois eventos?
• 3 - Como calcular a probabilidade da união de dois eventos?
• 4 - Videoaula: Como resolver questões de probabilidade no Enem?
• 5 - Exercícios resolvidos sobre probabilidade da união de dois eventos

Resumo da probabilidade da união de dois eventos

• A probabilidade da união de dois eventos A e B em um mesmo espaço amostral é calculada por: P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

• A probabilidade da união de dois eventos é a chance do primeiro ou do segundo evento ocorrer.

• Quando os eventos são mutuamente exclusivos, a probabilidade da união é calculada por: P(A ∪ B) = P(A) + P(B).

Qual a fórmula da probabilidade da união de dois eventos?

Dados dois eventos, A e B, todos em um mesmo espaço amostral Ω (lê-se: ômega), então a probabilidade da união desses eventos, ou seja, P(A ∪ B), é calculada por:

A fórmula diz que a probabilidade da união entre os eventos A e B é igual à probabilidade do evento A ocorrer, mais a probabilidade do evento B ocorrer, menos a probabilidade da intersecção entre os eventos A e B.

Existem casos em que os eventos são mutuamente exclusivos, ou seja, possuem intersecção vazia. Nesses casos, consequentemente, a probabilidade da intersecção será igual a zero, ou seja, P(A ∩ B) = 0. Portanto, quando os eventos são mutuamente exclusivos, a probabilidade da união desses eventos é calculada por:

Leia também: Probabilidade condicional — veja como calculá-la

Como calcular a probabilidade da união de dois eventos?

Para calcular a probabilidade da união de dois conjuntos, é necessário encontrar os dados para calcular cada uma das probabilidades. São eles:

• n(A) → número de elementos correspondentes ao evento A;

• n(B) → número de elementos correspondentes ao evento B;

• n(Ω) → número de elementos no espaço amostral;

• n(A ∩ B) → número de elementos na intersecção entre os eventos A e B.

Munidos desses dados, basta substituirmos na fórmula da probabilidade da união de dois eventos cada uma das probabilidades.

Exemplo 1

Em uma sala de aula, há 25 alunos, sendo que 15 deles são meninas e 10, meninos. Durante as aulas de matemática, o professor resolveu fazer um sorteio entre os alunos que se saíram melhor no teste. Sabendo que nessa sala há 8 alunos que usam óculos e que 3 deles são meninas, calcule a probabilidade de o sorteado ser uma menina ou alguém que usa óculos.

Resolução:

Inicialmente, vamos definir os eventos:

• A → o sorteado é uma menina.

• B → o sorteado usa óculos.

Sabemos que:

• n(A) é igual ao número de meninas.

  • n(A) = 15

• n(B) é igual ao número de alunos que usam óculos.

  • n(B) = 8

• n(Ω) → número de alunos.

  • n(Ω) = 25

• n(A ∩ B) → número de meninas que usam óculos.

  • n(A ∩ B) = 3

Então, temos que:

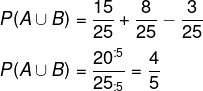
Exemplo 2:

Uma moeda foi lançada três vezes consecutivas. Qual é a probabilidade de se obter, exatamente, duas caras ou duas coroas?

Resolução:

Ao se lançar a moeda três vezes consecutivas, teremos os seguintes resultados possíveis:

Ω = {(cara, cara, cara); (cara, cara, coroa); (cara, coroa, cara); (coroa, cara, cara); (coroa, coroa, coroa); (coroa, coroa, cara); (coroa, cara, coroa); (cara, coroa, coroa)}

Logo, n (Ω) = 8.

• Evento A → Se obter exatamente duas caras.

A = {(cara, cara, coroa); (cara, coroa, cara); (coroa, cara, cara)}

n(A) = 3

• Evento B → Se obter exatamente duas coroas.

B = {(coroa, coroa, cara); (coroa, cara, coroa); (cara, coroa, coroa)}

n(B) = 3

Analisando os conjuntos A e B, é possível perceber que não há nenhum elemento em comum aos dois conjuntos. Logo, esses conjuntos são mutuamente excludentes. Desse modo, n(A ∩ B) = 0. Por fim, temos que:

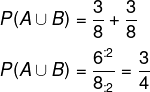
Videoaula: Como resolver questões de probabilidade no Enem?

Exercícios resolvidos sobre probabilidade da união de dois eventos

Questão 1

(Fepese) Sejam dois eventos, A e B, mutuamente exclusivos. A probabilidade de ocorrência de A vale 0,2. A probabilidade de ocorrência de B vale 0,4.

Quanto vale a probabilidade de ocorrência do evento A união B?

A) 0,08

B) 0,4

C) 0,48

D) 0,52

E) 0,6

Resolução:

Alternativa E

Sabemos que:

• P(A) = 0,2

• P(B) = 0,4

Como os eventos são mutuamente exclusivos, P(A ∩ B) = 0.

P(A ∪ B) = P(A) + P(B)

P(A ∪ B) = 0,2 + 0,4

P(A ∪ B) = 0,6

Questão 2

Dois dados são lançados simultaneamente, e o resultado é a soma das faces superiores. A probabilidade do resultado do lançamento ser maior que 9 ou um número primo é de:

A) 0,50

B) 0,58

C) 0,53

D) 0,65

E) 0,72

Resolução:

Alternativa C

Primeiramente, vamos construir o espaço amostral por meio de uma tabela:

Note que há 36 resultados distintos na tabela. Logo, n(Ω) = 36.

Agora, vamos definir os eventos:

• A → ser maior que 9

Analisando a tabela, há 6 resultados maiores que 9, então temos que n(A) = 6.

• B → ser um número primo

Analisando a tabela, os números primos são 2, 3, 5, 7 e 11. Calculando a quantidade de vezes em que cada um aparece, temos que n(B) = 15.

Analisando a intersecção, sabemos que 11 está sendo contado nos dois conjuntos, pois ele é um número primo e, também, maior que 9. Há duas maneiras diferentes de se chegar a 11 como resultado. Dessa forma, temos que:

n(A ∩ B) = 2

Então, calculando a probabilidade:

\(P(A∪B)= \frac{6}{36} + \frac{15}{36} - \frac{2}{36}\)

\(P(A∪B)= \frac{19}{36} = 0,5277 ... = 0,53\)