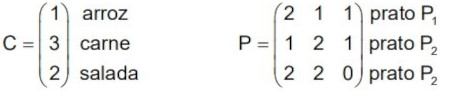A multiplicação de matrizes é feita por meio de um algoritmo que exige bastante atenção. Para que exista o produto entre a matriz A e a matriz B, é necessário que o número de colunas da primeira matriz, no caso A, seja igual ao número de linhas da segunda matriz, no caso B.
A partir da multiplicação entre matrizes, é possível compreender o que é a matriz identidade, que é o elemento neutro da multiplicação de matrizes, e o que é a matriz inversa da matriz M, que é a matriz M-1 cujo produto de M por M-1 é igual à matriz identidade. Também é possível a multiplicação de uma matriz por um número real — nesse caso, multiplicamos cada um dos termos da matriz pelo número.
Leia também: O que é uma matriz triangular?
Tópicos deste artigo
- 1 - Condição de existência
- 2 - Como calcular o produto entre duas matrizes?
- 3 - Matriz identidade
- 4 - O que é a matriz inversa?
- 5 - Multiplicação da matriz por um número real
- 6 - Exercícios resolvidos
Condição de existência

Para multiplicar duas matrizes, primeiramente é necessário verificar a condição de existência. Para que o produto exista, o número de colunas da primeira matriz tem que ser igual ao número de linhas da segunda matriz. Além disso, o resultado da multiplicação é uma matriz que possui o mesmo número de linhas da primeira matriz e o mesmo número de colunas da segunda matriz.
Por exemplo, o produto AB entre as matrizes A3x2 e B2x5 existe, pois o número de colunas de A (2 colunas) é igual ao número de linhas de B (2 linhas), e o resultado é a matriz AB3x5. Já produto entre as matrizes C3x5 e a matriz D2x5 não existe, pois C possui 5 colunas e D possui 3 linhas.
Como calcular o produto entre duas matrizes?
Para realizar a multiplicação de matrizes, é necessário seguir algumas passos. Faremos um exemplo da multiplicação de uma matriz algébrica A2x3 pela matriz B3x2
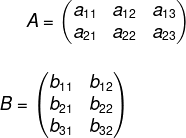
Sabemos que o produto existe, pois a matriz A possui 3 colunas, e a matriz B, 3 linhas. Chamaremos de C o resultado da multiplicação A·B. Além disso, também sabemos que o resultado é uma matriz C2x2, pois a matriz A tem 2 linhas, e a matriz B, 2 colunas.
Para calcular o produto entre a matriz A2x3 e a matriz B3x2, vamos seguir alguns passos.
Primeiramente encontraremos cada um dos termos da matriz C2x2:
![]()
Para encontrar os termos, vamos relacionar sempre as linhas da matriz A com as colunas da matriz B:
c11 → 1ª linha de A e 1ª coluna de B
c12 → 1ª linha de A e 2ª coluna de B
c21 → 2ª linha de A e 1ª coluna de B
c22 → 2ª linha de A e 2ª coluna de B
Calculamos cada um dos termos fazendo a multiplicação entre os termos da linha de A e os termos da coluna de B. Agora devemos somar esses produtos, começando por c11:
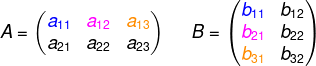
1ª linha de A
1ª coluna de B
c11 = a11·b11 + a12·b21 + a13·b31
Calculando c12:
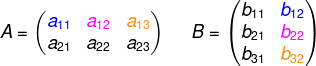
1ª linha de A
2ª coluna de B
c12 = a11·b12 + a12·b22+a13·b32
Calculando c21:
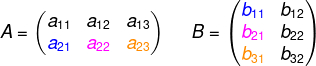
2ª linha de A
1ª coluna de B
c21 = a21·b11 + a22·b21+a23·b31
Calculando o termo c22:
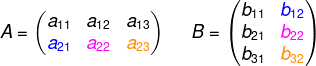
2ª linha de A
2ª coluna de B
c22 = a21·b12 + a22·b22+a23·b32
Sendo assim, a matriz C é formada pelos termos:
![]()
Exemplo:
Vamos calcular a multiplicação entre as matrizes A e B.
![]()
Sabemos que, em A2x2 e B2x3, o número de colunas da primeira é igual ao número de linhas da segunda, então o produto existe. Assim, faremos C = A· B e sabemos que C2x3.
Multiplicando, temos que:
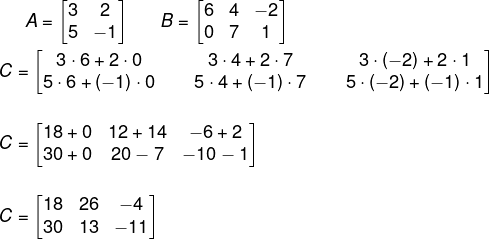
Veja também: O que é uma matriz transposta?
Matriz identidade
Na multiplicação entre matrizes, existem alguns casos especiais, como a matriz identidade, que é o elemento neutro da multiplicação entre matrizes. A matriz identidade é uma matriz quadrada, ou seja, o número de linhas é sempre igual ao número de colunas. Além disso, nela somente os termos da diagonal são iguais a 1, e os demais termos são todos iguais a zero. Quando multiplicamos uma matriz M pela matriz identidade In, temos que:
M · In = M
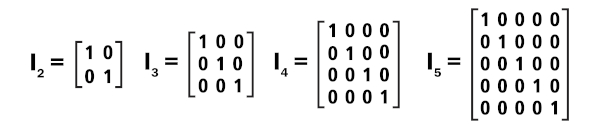
Exemplo:
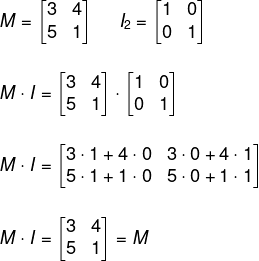
O que é a matriz inversa?
Dada uma matriz M, conhecemos como matriz inversa de M a matriz M-1 cujo produto M · M-1 é igual à matriz identidade In. Para que uma matriz tenha inversa, ela precisa ser quadrada, e seu determinante tem que ser diferente de 0. Vejamos exemplos de matrizes que são inversas:
![]()
Calculando o produto A·B, temos que:
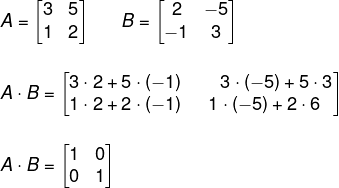
Note que o produto entre A e B gerou a matriz I2. Quando isso acontece, dizemos que B é a matriz inversa de A. Para saber mais detalhes sobre esse tipo de matriz, leia: Matriz inversa.
Multiplicação da matriz por um número real
Diferente da multiplicação entre matrizes, existe também a multiplicação da matriz por um número real, que é uma operação bem mais simples de encontrar a solução.
Dada uma matriz M, a multiplicação da matriz por um número real k é igual à matriz kM. Para encontrar essa matriz kM, basta multiplicar todos os termos da matriz pela constante k.
Exemplo:
Se k = 5 e considerando a matriz M a seguir, encontre a matriz 5M.
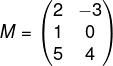
Multiplicando:
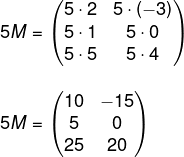
Exercícios resolvidos
Questão 1 - (Unitau) Dadas as matrizes A e B,
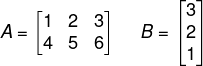
o valor do elemento c11 da matriz C = AB é:
A) 10.
B) 28.
C) 38.
D) 18.
E) 8.
Resolução
Alternativa A.
Como queremos o termo c11, vamos multiplicar os termos da primeira linha e de A com os termos da primeira coluna de B.
Calculando c11 = 1 · 3 + 2 · 2 + 3 · 1 = 3 + 4 + 3 = 10
Questão 2 - (Enem 2012) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4×4, e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir.
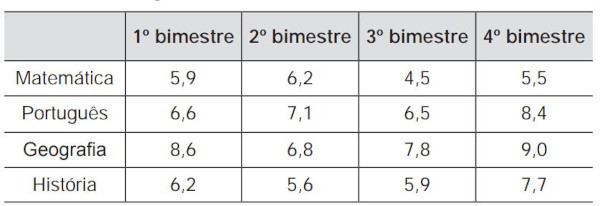
Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela pela matriz:
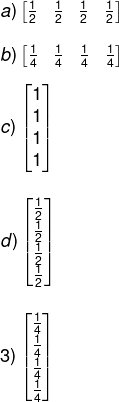
Resolução
Alternativa E.
A média nada mais é do que a soma dos elementos dividida pela quantidade de elementos. Note que há 4 notas por linha, então a média seria a soma dessas notas dividida por 4. Dividir por 4 é o mesmo que multiplicar pela fração ¼. Além disso, a matriz das notas é uma matriz 4x4, então temos que multiplicar por uma matriz 4x1, ou seja, que possui 4 linhas e 1 coluna, para encontrar a matriz que tem a média das notas.
Por Raul Rodrigues de Oliveira
Professor de Matemática