A matriz é comumente utilizada para a organização de dados tabulares a fim de facilitar a resolução de problemas. As informações das matrizes, sejam estas numéricas ou não, são dispostas organizadamente em linhas e colunas.
O conjunto das matrizes munido das operações de adição, subtração e multiplicação e de características, como elemento neutro e inverso, forma uma estrutura matemática que possibilita sua aplicação em diversos campos dessa grande área do conhecimento.
Veja também: Relação entre matriz e sistemas lineares
Tópicos deste artigo
- 1 - Representação de matrizes
- 2 - Tipos de matrizes
- 3 - Matriz oposta
- 4 - Operações com matrizes
- 5 - Exercícios resolvidos
Representação de matrizes
Antes de começarmos os estudos sobre matrizes, é necessário estabelecer algumas notações quanto às suas representações. As matrizes são sempre representadas por letras maiúsculas (A, B, C…), que são acompanhadas por índices, nos quais o primeiro número indica a quantidade de linhas, e o segundo, o número de colunas.
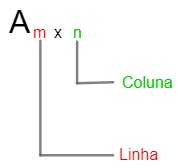
A quantidade de linhas (fileiras horizontais) e colunas (fileiras verticais) de uma matriz determina sua ordem. A matriz A possui ordem m por n. As informações contidas em uma matriz são chamadas de elementos e ficam organizadas entre parênteses, colchetes ou duas barras verticais, veja os exemplos:
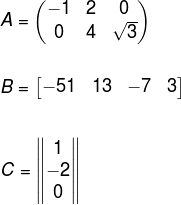
A matriz A possui duas linhas e três colunas, logo, sua ordem é dois por três → A2x3.
A matriz B possui uma linha e quatro colunas, logo, sua ordem é um por quatro, por isso recebe o nome de matriz linha → B1x4.
A matriz C possui três linhas e uma coluna, e por isso é chamada de matriz coluna e sua ordem é três por um → C3x1.
Podemos representar genericamente os elementos de uma matriz, isto é, podemos escrever esse elemento utilizando uma representação matemática. O elemento genérico será representado por letras minúsculas (a, b, c…), e, assim como na representação de matrizes, ele também possui índice que indica sua localização. O primeiro número indica a linha em que o elemento está, e o segundo número indica a coluna na qual ele se localiza.
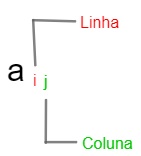
Considere a seguinte matriz A, faremos a listagem de seus elementos.
![]()
Observando o primeiro elemento que está localizado na primeira linha e primeira coluna, ou seja, na linha um e coluna um, temos o número 4. A fim de facilitar a escrita, vamos denotá-lo por:
a11 → elemento da linha um, coluna um
Assim temos os seguintes elementos da matriz A2x3:
a11 = 4
a12 =16
a13 = 25
a21 = 81
a22 = 100
a23 = 9
De modo geral, podemos escrever uma matriz em função de seus elementos genéricos, essa é a matriz genérica.
Uma matriz de m linha e n colunas é representada por:
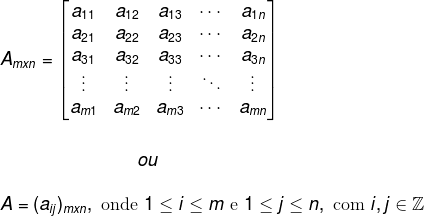
-
Exemplo
Determine a matriz A = [aij ]2x2, que possui a seguinte lei de formação aij = j2 – 2i. Dos dados do enunciado, temos que a matriz A é de ordem dois por dois, ou seja, possui duas linhas e duas colunas, logo:
![]()
Além disso, foi dada a lei de formação da matriz, ou seja, a cada elemento satisfaz-se a relação aij = j2 – 2i. Substituindo os valores de i e j na fórmula, temos:
a11 = (1)2 - 2(1) = -1
a12 = (2)2 - 2(1) = 2
a21 = (1)2 - 2(2) = -3
a22 = (2)2 - 2(2) = 0
Portanto, a matriz A é:
![]()
Tipos de matrizes
Algumas matrizes merecem uma atenção especial, veja agora esses tipos de matrizes com exemplos.
-
Matriz quadrada
Uma matriz é quadrada quando o número de linhas é igual ao número de colunas. Representamos a matriz que possui n linhas e n colunas por An (lê-se: matriz quadrada de ordem n).
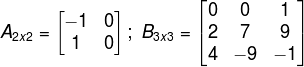
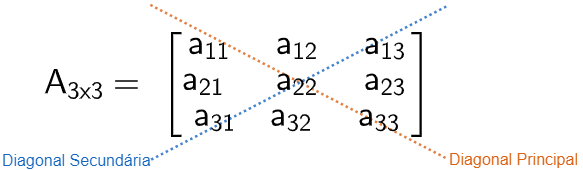
Nas matrizes quadradas, temos dois elementos muito importantes, as diagonais: principal e secundaria. A diagonal principal é formada por elementos que possuem índices iguais, ou seja, é todo elemento aij com i = j. A diagonal secundária é formada por elementos aij com i + j = n +1, em que n é ordem da matriz.
-
Matriz identidade
A matriz identidade é uma matriz quadrada que possui todos os elementos da diagonal principal iguais a 1 e os demais elementos iguais a 0, sua lei de formação é:
![]()
Denotamos essa matriz por I, em que n é a ordem da matriz quadrada, veja alguns exemplos:
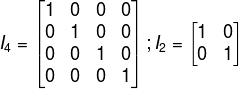
-
Matriz unitária
É uma matriz quadrada de ordem um, ou seja, possui uma linha e uma coluna e, portanto, apenas um elemento.
A = 1X1, B = I1 = (1)1X1 e C = || 5||1X1
Essas são exemplos de matrizes unitárias, com destaque para matriz B, que é uma matriz de identidade unitária.
-
Matriz nula
Uma matriz é dita nula se todos os seus elementos são iguais a zero. Representamos uma matriz nula de ordem m por n por Omxn.
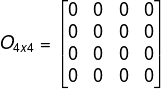
A matriz O é nula de ordem 4.
-
Matriz oposta
Considere duas matrizes de ordens iguais: A = [aij]mxn e B = [bij]mxn. Essas matrizes serão chamadas de opostas se, e somente se, aij = -bij. Desse modo, os elementos correspondentes devem ser números opostos.
Podemos representar a matriz B = -A.
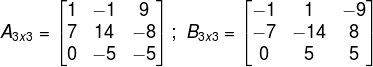
-
Matriz transposta
Duas matrizes A = [aij]mxn e B = [bij]nxm são transpostas se, e somente se, aij = bji , ou seja, dado uma matriz A, para encontrar sua transposta, basta tomar as linhas como colunas.
A transposta da matriz A é denotada por AT. Veja o exemplo:
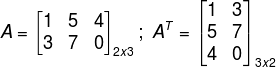
Veja mais: Matriz inversa: o que é e como verificar
Operações com matrizes
O conjunto das matrizes possui as operações de adição e multiplicação muito bem definidas, isto é, sempre que operamos duas ou mais matrizes, o resultado da operação ainda pertence ao conjunto das matrizes. No entanto, e a operação de subtração? Essa operação entendemos como sendo a inversa da adição (matriz oposta), que também está muito bem definida.
Antes de definirmos as operações, vamos entender as ideias de elemento correspondente e igualdade de matrizes. Elementos correspondentes são aqueles que ocupam a mesma posição em diferentes matrizes, ou seja, que estão localizados na mesma linha e coluna. Obviamente as matrizes precisam ser de mesma ordem para que existam elementos correspondentes. Veja:
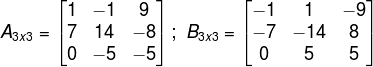
Os elementos 14 e -14 são elementos correspondes das matrizes opostas A e B, pois ocupam a mesma posição (mesma linha e coluna).
Duas matrizes vão ser ditas iguais se, e somente se, os elementos correspondentes são iguais. Assim, dadas as matrizes A = [aij]mxn e B = [bij]mxn, essas vão ser iguais se, e somente se, aij = bij para quaisquer i j.
-
Exemplo
Sabendo que as matrizes A e B são iguais, determine os valores de x e t.
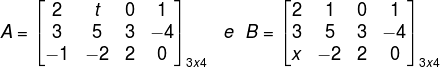
Como as matrizes A e B são iguais, então os elementos correspondentes devem ser iguais, portanto:
x = -1 e t = 1
-
Adição e subtração de matrizes
As operações de adição e subtração entre matrizes são bastante intuitivas, mas antes é necessário que uma condição seja satisfeita. Para realizar essas operações, antes é necessário verificar se as ordens das matrizes são iguais.
Verificado essa condição, a adição e subtração de matriz dá-se somando ou subtraindo os elementos correspondentes das matrizes. Considere as matrizes A = [aij]mxn e B = [bij]mxn, então:
A + B = [aij + bij] mxn
A – B = [aij – bij] mxn
-
Exemplo
Considere as matrizes A e B a seguir, determine A + B e A – B.
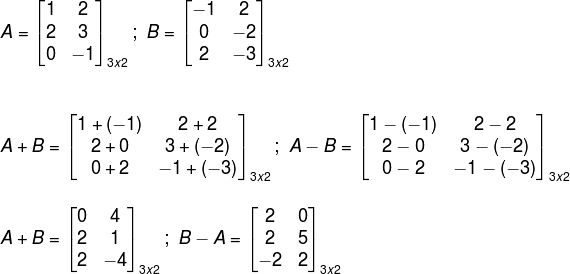
Leia também: Operações com números inteiros
-
Multiplicação de um número real por matriz
A multiplicação de um número real de uma matriz (também conhecida como multiplicação de matriz) por uma escalar é dada multiplicando cada elemento da matriz pela escalar.
Seja A = [aij]mxn uma matriz e t um número real, então:
t · A = [t · aij]mxn
Veja o exemplo:
![]()
-
Multiplicação de matrizes
A multiplicação de matrizes não é tão trivial quanto a adição e subtração delas. Antes de realizar a multiplicação, uma condição deve também ser satisfeita em relação à ordem das matrizes. Considere as matrizes Amxn e Bnxr.
Para realizar a multiplicação, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda. A matriz produto (que vem da multiplicação) possui ordem dada pela quantidade de linhas da primeira e quantidade de colunas da segunda.
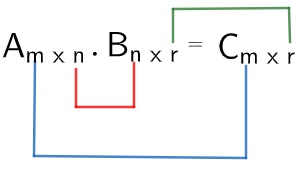
Para efetuar a multiplicação entre as matrizes A e B, devemos multiplicar cada uma das linhas por todas as colunas da seguinte maneira: o primeiro elemento de A é multiplicado pelo primeiro elemento de B e, em seguida, somado ao segundo elemento de A e multiplicado pelo segundo elemento de B, e assim sucessivamente. Veja o exemplo:
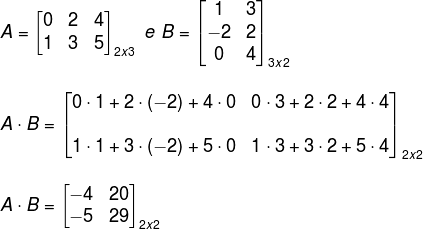
Leia também: Teorema de Laplace: saiba como e quando usar
Exercícios resolvidos
Questão 1 – (U. E. Londrina – PR) Sejam as matrizes A e B, respectivamente, 3 x 4 e p x q, e se a matriz A · B possui ordem 3 x 5, então é verdade que:
a) p = 5 e q = 5
b) p = 4 e q = 5
c) p = 3 e q = 5
d) p = 3 e q = 4
e) p = 3 e q = 3
Solução
Temos do enunciado que:
A3X4 · Bpxq = C3x5
Da condição para multiplicar duas matrizes temos que o produto só existe se o número de colunas da primeira for igual ao número de linhas da segunda, logo, p = 4. E sabemos também que a matriz produto é dada pela quantidade de linhas da primeira com a quantidade de colunas da segunda, logo, q = 5.
Portanto, p = 4 e q = 5.
R: Alternativa b
Questão 2 – (Vunesp) Determine os valores de x, y e z, na igualdade a seguir, envolvendo matrizes reais 2 x 2.
![]()
Solução
Vamos realizar as operações entre as matrizes e, em seguida, a igualdade entre elas.
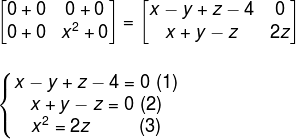
Para determinar o valor de x, y e z, resolveremos o sistema linear. Inicialmente vamos somar as equações (1) e (2).
2x – 4= 0
2x = 4
x = 2
Substituindo o valor de x encontrado na equação (3), temos:
22 = 2z
2z = 4
z = 2
E por fim, substituindo os valores de x e z encontrados na equação (1) ou (2), temos:
x + y – z = 0
2 +y – 2 = 0
y =0
Portanto, a solução do problema é dada por S = {(2, 0, 2)}.






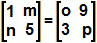 .
.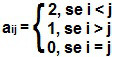
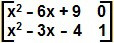 igual à matriz identidade de ordem 2, o valor de 2.x é:
igual à matriz identidade de ordem 2, o valor de 2.x é: