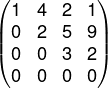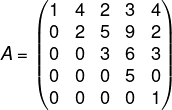Matriz triangular

Uma matriz é triangular quando os elementos que estão acima da diagonal principal ou os elementos que estão abaixo da diagonal principal são todos nulos. Existem duas classificações possíveis para esse tipo de matriz: a primeira é quando os elementos que estão acima da diagonal principal são nulos, o que configura uma matriz triangular inferior; a segunda é quando os elementos que estão abaixo da diagonal principal são nulos, configurando uma matriz triangular superior.

Para calcular o determinante de uma matriz triangular pela regra de Sarrus, basta realizar a multiplicação da diagonal principal, já que as outras multiplicações serão todas iguais a zero.

Leia também: Matriz — o que é e tipos existentes

Tópicos deste artigo

• 1 - Tipos de matriz triangular
• 2 - Matriz diagonal
• 3 - Determinante de uma matriz triangular
• 4 - Propriedades da matriz triangular
• 5 - Exercícios resolvidos

Tipos de matriz triangular

Para compreender o que é uma matriz triangular, é importante lembrar o que é a diagonal principal de uma matriz quadrada, que é a matriz que possui o mesmo número de linhas e colunas. A diagonal principal da matriz são os termos a_ij, em que i = j, ou seja, são os termos em que o número da linha é igual ao número da coluna.

Exemplo:

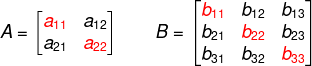
Entendendo o que é uma matriz quadrada e qual é a sua diagonal principal, vamos conhecer o que é uma matriz triangular e as suas classificações. Existem duas classificações possíveis para a matriz triangular: a matriz triangular inferior e a matriz triangular superior.

• Matriz triangular inferior: ocorre quando todos os termos que estão acima da diagonal principal são iguais a zero e os termos que estão abaixo da diagonal principal são números reais.

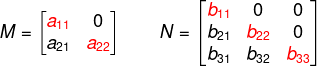
Exemplo numérico:

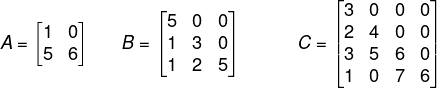
• Matriz triangular superior: ocorre quando todos os termos que estão abaixo da diagonal principal são iguais a zero e os termos que estão acima da diagonal principal são números reais.

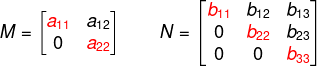
Exemplo numérico:

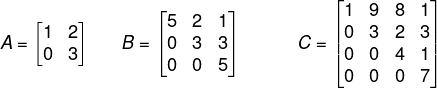
Matriz diagonal

A matriz diagonal é um caso particular de matriz triangular. Nela os únicos termos que são diferentes de zero são aqueles que estão contidos na diagonal principal. Já os termos que estão acima ou abaixo da diagonal principal são todos iguais a zero.

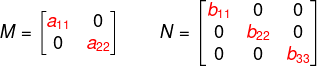
Exemplos numéricos de matriz diagonal:

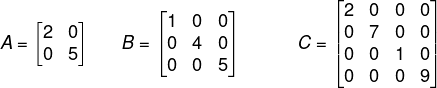
Determinante de uma matriz triangular

Dada uma matriz triangular, ao calcular o determinante dessa matriz pela regra de Sarrus, é possível perceber que todas as multiplicações são iguais a zero, exceto a multiplicação do termo da diagonal principal.

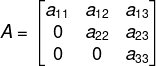
det(A) = a₁₁ · a₂₂· a₃₃ + a₁₂ · a₂₃ · 0 + a₁₃ · 0 · 0  – ( a₁₃ · a₂₃ · 0 +  a₁₁ · a₂₃ · 0 + a₁₂ · 0 · a₃₃)

Note que, em todos os termos, exceto no primeiro, o zero é um dos fatores, e toda multiplicação por zero é igual a zero, logo:

det(A) =  a₁₁ · a₂₂· a₃₃  

Veja que esse é o produto entre os termos da diagonal principal.

Independentemente do número de linhas e colunas que uma matriz triangular tiver, o seu determinante será sempre igual ao produto dos termos da diagonal principal.

Veja também: Determinante — recurso aplicado a matrizes quadradas

Propriedades da matriz triangular

A matriz triangular possui algumas propriedades específicas.

• 1ª propriedade: o determinante de uma matriz triangular é igual ao produto dos termos da diagonal principal.
• 2ª propriedade: o produto entre duas matrizes triangulares é uma matriz triangular.
• 3ª propriedade: se um dos termos da diagonal principal da matriz triangular for igual a zero, então o seu determinante será igual a zero e, consequentemente, ela não será inversível.
• 4ª propriedade: a matriz inversa de uma matriz triangular é também uma matriz triangular.
• 5ª propriedade: a soma de duas matrizes triangulares superiores é uma matriz triangular superior; de forma análoga, a soma de duas matrizes triangulares inferiores é uma matriz triangular inferior.

Exercícios resolvidos

1) Dada a matriz A, o valor do determinante de A é:

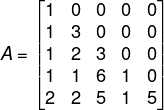
a) 2

b) 0

c) 9

d) 45

e) 25

Resolução

Alternativa d.

Essa matriz é triangular inferior, então o determinante dela é a multiplicação dos termos da diagonal principal.

det(A) = 1·3·3·1·5 = 45

2) Julgue as afirmativas a seguir.

I → Toda matriz quadrada é triangular.

II → A soma de uma matriz triangular superior com uma matriz triangular inferior sempre é uma matriz triangular.

III → Toda matriz diagonal identidade é uma matriz triangular.

A ordem correta é:

a) V, V, V.

b) F, F, F.

c) F, V, F.

d) F, F, V.

e) V, V, F.

Resolução

Alternativa d.

I → Falsa, pois toda matriz triangular é quadrada, mas nem toda matriz quadrada é triangular.

II → Falsa, pois a soma entre uma matriz triangular superior e outra triangular inferior nem sempre resulta em uma matriz triangular.

III → Verdadeira, pois os termos diferentes da diagonal são iguais a zero.

Por Raul Rodrigues de Oliveira
Professor de Matemática