A matriz transposta da matriz M é a matriz Mt. Trata-se da matriz que vamos obter quando reescrevemos a matriz M trocando de posição as linhas e colunas, transformando a primeira linha de M na primeira coluna de Mt, a segunda linha de M na segunda coluna de Mt, e assim sucessivamente.
Se a matriz M possui m linhas e n colunas, a sua matriz transposta, ou seja, Mt, vai possuir n linhas e m colunas. Existem propriedades específicas para a matriz transposta.
Leia também: O que é uma matriz triangular?
Tópicos deste artigo
- 1 - Como é obtida a matriz transposta?
- 2 - Matriz simétrica
- 3 - Propriedades da matriz transposta
- 4 - Matriz inversa
- 5 - Matriz oposta
- 6 - Exercícios resolvidos
Como é obtida a matriz transposta?
Dada uma matriz Am x n, conhecemos como a matriz transposta de A a matriz Atn x m. Para encontrar a matriz transposta, basta trocar a posição das linhas e colunas da matriz A. O que for a primeira linha da matriz A será a primeira coluna da matriz transposta At, a segunda linha da matriz A será a segunda coluna da matriz At, e assim sucessivamente.
De forma algébrica, seja M = (mij)m x n , a matriz transposta de M é Mt = (mji) n x m.
Exemplo:
Encontre a matriz transposta da matriz:
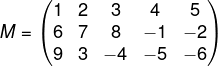
A matriz M é uma matriz 3x5, então a sua transposta será 5x3. Para encontrar a matriz transposta, faremos com que a primeira linha da matriz M seja a primeira coluna da matriz Mt.
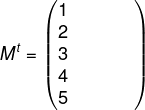
A segunda linha da matriz M será a segunda coluna da matriz transposta:
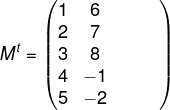
Por fim, a terceira linha da matriz M se tornará a terceira coluna da matriz Mt:
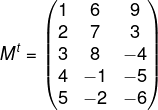
Matriz simétrica
Com base no conceito de matriz transposta, é possível definir o que é uma matriz simétrica. Uma matriz é conhecida como simétrica quando ela é igual à sua matriz transposta, ou seja, dada a matriz M, M = Mt.
Para que isso aconteça, a matriz precisa ser quadrada, o que significa que, para que a matriz seja simétrica, o número de linhas deve ser igual ao número de colunas.
Exemplo:
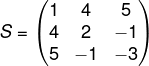
Quando analisamos os termos acima da diagonal principal e os termos abaixo da diagonal principal da matriz S, é possível perceber que há termos que são iguais, o que faz com que ela seja conhecida como simétrica exatamente pela simetria da matriz em relação à diagonal principal.
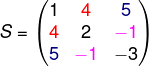
Se encontrarmos a transposta da matriz S, é possível perceber que St é igual a S.
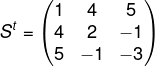
Como S = St, essa matriz é uma simétrica.
Veja também: Como resolver os sistemas lineares?
Propriedades da matriz transposta
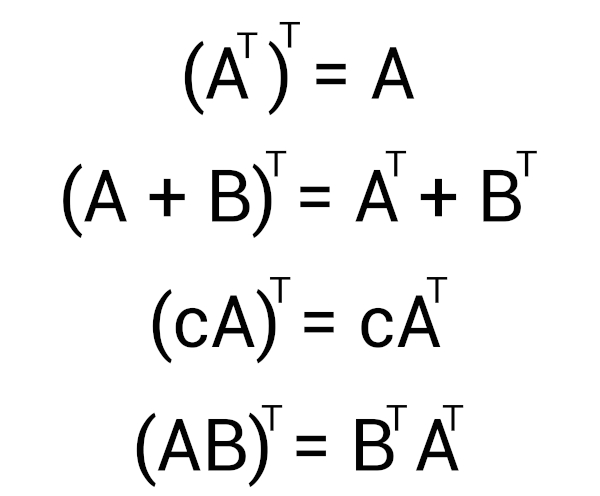
-
1ª propriedade: a transposta de uma matriz transposta é igual à própria matriz:
(Mt)t = M
-
2ª propriedade: a transposta da soma entre as matrizes é igual à soma da transposta de cada uma das matrizes:
(M + N)t = Mt + Nt
-
3ª propriedade: a transposta da multiplicação entre duas matrizes é igual à multiplicação da transposta de cada uma das matrizes:
(M · N)t = Mt · Nt
-
4ª propriedade: o determinante da matriz é igual ao determinante da matriz transposta:
det(M) = det(Mt)
-
5ª propriedade: a transposta da matriz vezes a constante é igual à matriz transposta vezes a constante:
(kA)t = kAt
Matriz inversa
O conceito de matriz inversa é bem diferente do conceito de matriz transposta, e é importante ressaltar a diferença entre eles. A matriz inversa de uma matriz M é a matriz M-1, em que o produto entre as matrizes M e M-1 é igual à matriz identidade.
Exemplo:
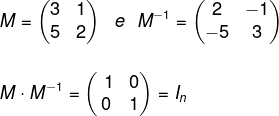
Para conhecer melhor esse tipo de matriz, leia o nosso texto: Matriz inversa.
Matriz oposta
Sendo outro caso de matriz especial, a matriz oposta da matriz M é a matriz -M. Conhecemos como matriz oposta de M = (mij) a matriz -M = (-mij). A matriz oposta é composta pelos termos opostos da matriz M.
![]()
Exercícios resolvidos
Questão 1 – (Cesgranrio) Considere as matrizes:
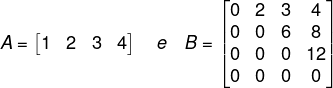
Denotamos por At a matriz transposta de A. A matriz (AtA) – (B+Bt) é:
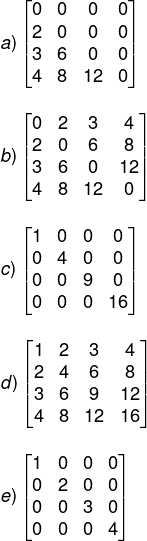
Resolução
Alternativa C
Primeiro encontraremos a matriz At e a matriz Bt:
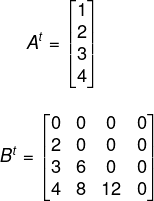
Então, temos que:
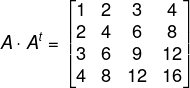
Agora calculamos B + Bt:
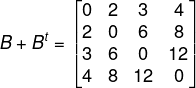
Por fim calcularemos a diferença entre A· At e B + Bt:
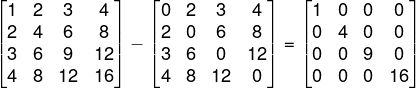
Questão 2 – (Cotec – adaptada) Dada as matrizes A e B multiplicando A · Bt, obtemos:
![]()
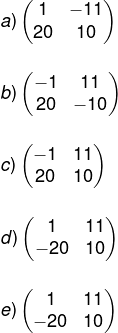
Resolução
Alternativa C
Primeiro encontraremos a matriz transposta de B:
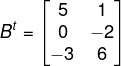
O produto entre as matrizes A e Bt é igual a:
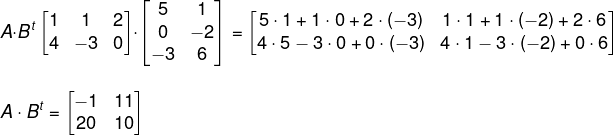
Por Raul Rodrigues de Oliveira
Professor de Matemática
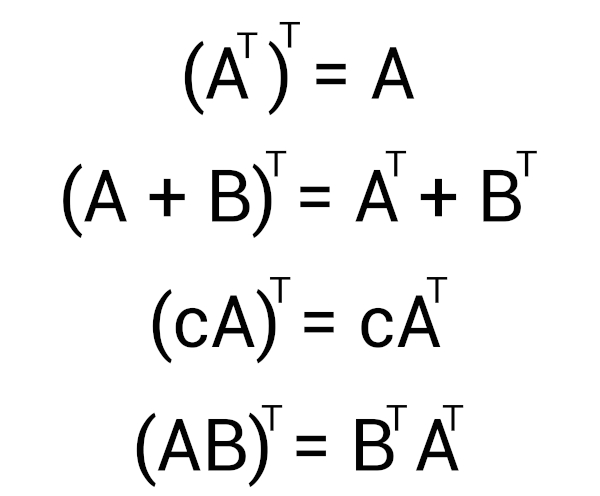


 e B =
e B = 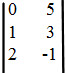 , determine:
, determine: e B =
e B = 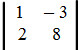
 , sendo At sua transposta, o determinante da matriz A.At
, sendo At sua transposta, o determinante da matriz A.At