A operação com qualquer matriz sempre resultará em outra matriz, independentemente da operação utilizada.
Antes de falarmos da adição e da subtração de matrizes, iremos relembrar do que uma matriz é formada: toda matriz tem seus elementos que são dispostos em linhas e colunas.
A quantidade de linhas e colunas deve ser maior ou igual a 1. Cada elemento vem representado com a linha e a coluna que pertence. Exemplo: Dada uma matriz B de ordem 2 x 3 o elemento que se encontra na 1º linha e 2° coluna será representado por b12.
►Adição
As matrizes envolvidas na adição devem ser da mesma ordem. E o resultado dessa soma será também outra matriz com a mesma ordem.
Assim podemos concluir que:
Se somarmos a matriz A com a matriz B de mesma ordem, A + B = C, teremos como resultado outra matriz C de mesma ordem e para formar os elementos de C somaremos os elementos correspondentes de A e B, assim: a11 + b11 = c11.
Exemplos:
Dada a matriz A= 


.jpg) =
= .jpg) 3 x 3
3 x 3
Observe os elementos em destaques:
a13 = - 1 e b13 = - 5 ao somarmos esses elementos chegaremos a um terceiro que é o
c13 = -6. Pois -1 + (-5) = -1 – 5 = - 6
O mesmo ocorre com os outros elementos, para chegarmos ao elemento c32, tivemos que somar a32 + b32. Pois, 3 + (-5) = 3 – 5 = - 2
Assim: A + B = C, onde C tem a mesma ordem de A e B.
►Subtração
As duas matrizes envolvidas na subtração devem ser da mesma ordem. E a diferença delas deverá dar como resposta outra matriz, mas de mesma ordem.
Assim temos:
Se subtrairmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim: a21 – b21 = c21.
Exemplos:
Dada a matriz A = 


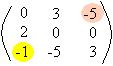

Observe os elementos destacados:
Quando subtraímos a13 – b13 = c13, -1 – (-5) = -1 + 5 = 4
Quando subtraímos a31 – b31 = c31, - 4 – (-1) = -4 + 1 = -3
Assim A – B = C, onde C é uma matriz de mesma ordem de A e B.
Por Danielle de Miranda
Graduada em Matemática


 ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.