Regra de Sarrus

Toda matriz quadrada pode ser associada a um número, que é obtido a partir de cálculos efetuados entre os elementos dessa matriz. Esse número é chamado de determinante.

A ordem da matriz quadrada é que determina o melhor método para o cálculo de seu determinante. Para matrizes de ordem 2, por exemplo, basta encontrar a diferença entre o produto dos elementos da diagonal principal pelo produto dos elementos da diagonal secundária. Para matrizes 3x3, podemos aplicar a regra de Sarrus ou ainda o Teorema de Laplace. Vale lembrar que esse último pode ser utilizado também para o cálculo de determinantes de matrizes quadradas de ordem superior a 3. Em casos específicos, o cálculo do determinante pode ser simplificado através apenas de algumas propriedades do determinante.

Para entender como é feito o cálculo do determinante com a regra de Sarrus, considere a seguinte matriz A de ordem 3:

Representação de uma matriz de ordem 3

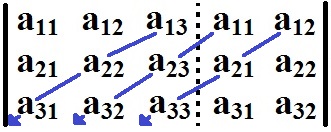
Inicialmente, as duas primeiras colunas são repetidas à direita da matriz A:

Devemos repetir as duas primeiras colunas à direita da matriz

Em seguida, os elementos da diagonal principal são multiplicados. Esse processo deve ser feito também com as diagonais que estão à direita da diagonal principal para que seja possível somar os produtos dessas três diagonais:

det A_p = a₁₁.a₂₂.a₃₃ + a₁₂.a₂₃.a₃₁ + a₁₃.a₂₁.a₃₂

Devemos somar os produtos das diagonais principais

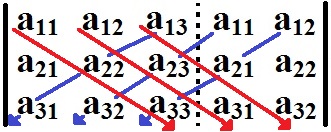
O mesmo processo deve ser realizado com a diagonal secundária e as demais diagonais à sua direita. Entretanto, é necessário subtrair os produtos encontrados:

det A_s = – a₁₃.a₂₂.a₃₁ – a₁₁.a₂₃.a₃₃ – a₁₂.a₂₁.a₃₃

Devemos subtrair os produtos das diagonais secundárias

Unindo os dois processos, é possível encontrar o determinante da matriz A:

det A = det A_p + det A_s

det A = a₁₁.a₂₂.a₃₃ + a₁₂.a₂₃.a₃₁ + a₁₃.a₂₁.a₃₂ – a₁₃.a₂₂.a₃₁ – a₁₁.a₂₃.a₃₃ – a₁₂.a₂₁.a₃₃

Representação da aplicação da Regra de Sarrus

Veja agora o cálculo do determinante da seguinte matriz B de ordem 3x3:

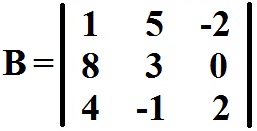
Cálculo do determinante da matriz B através da Regra de Sarrus

Através da regra de Sarrus, o cálculo do determinante da matriz B será feito da seguinte forma:

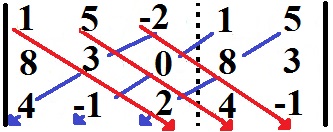
Aplicando a regra de Sarrus para encontrar o determinante da Matriz B

det B = b₁₁.b₂₂.b₃₃ + b₁₂.b₂₃.b₃₁ + b₁₃.b₂₁.b₃₂ – b₁₃.b₂₂.b₃₁ – b₁₁.b₂₃.b₃₃ – b₁₂.b₂₁.b₃₃

det B = 1.3.2 + 5.0.4 + (–2).8.(–1) – (–2).3.4 – 1.0.(–1) – 5.8.2

det B = 6 + 0 + 16 – (–24) – 0 – 80

det B = 22 – 56

det B = – 34

Portanto, pela Regra de Sarrus, o determinante da matriz B é – 34.

Por Amanda Gonçalves
Graduada em Matemática