Exemplo 1
Paulo aplicou R$ 800,00 num investimento que rende 3% a.m., a juros compostos. Quanto tempo após a aplicação o saldo será de R$ 1.200,00?
.jpg)
Exemplo 2
Em uma determinada cidade a taxa de crescimento populacional e de 4% ao ano, aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 (1,04) = P1
População após dois anos = P0 (1,04)² = P2
População após x anos = P0 (1,04)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, temos:
Exemplo 3
Em quanto tempo 800 g de uma certa substância radioativa, que se desintegra a uma taxa de 2% ao ano, se reduzirá a 200 g? Use:
.jpg){kind=small}
em que Q é a massa da substância, r é a taxa e t é o tempo em anos.
.jpg)
Por Marcos Noé
Graduado em Matemática
De estudante para estudante
Lista de exercícios
Considerando-se que x = 21000 e sabendo que log2 é aproximadamente igual a 0,30103, determine o número de algarismos de x.
Um líquido volátil diminui seu volume na ordem de 20% por hora. O seu volume se reduzirá à metade durante um tempo t. Considerando essas condições, determine aproximadamente o tempo t. (Dado log2 = 0,3)
Determine o número real x que satisfaz a equação log2(12 – 2x) = 2x.
(Vunesp – SP) O corpo de uma vítima de assassinato foi encontrado às 22h. Às 22h 30min o médico da polícia chegou e imediatamente tomou a temperatura do cadáver, que era de 32,5 ºC. Uma hora mais tarde, tomou a temperatura outra vez e encontrou 31,5 ºC. A temperatura do ambiente foi mantida constante a 16,5 ºC. Admita que a temperatura normal de uma pessoa viva seja de 36,5 ºC e suponha que a lei matemática que descreve o resfriamento do corpo é dada por D(t) = D0 * 2(−2αt), em que t é o tempo em horas, D0é a diferença de temperatura do cadáver com o meio no instante t = 0, D(t) é a diferença de temperatura do cadáver com o meio ambiente num instante t qualquer e α é uma constante positiva. Os dados obtidos pelo médico foram colocados na tabela seguinte:
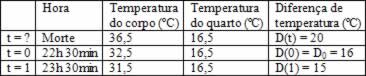
Considerando os valores aproximados log25 = 2,3 e log23 – 1,6, determine:
a) a constante α
b) a hora em que a pessoa morreu.