Em vários cálculos de logaritmos ou operações envolvendo logaritmos é preciso transformar a base do logaritmo em outra, para facilitar as operações.
Para ocorrer essas transformações é preciso obedecer algumas regras e propriedades operatórias dos logaritmos.
Dado o logaritmo loga x = y de base a, para transformar o mesmo logaritmo para a base b, o logaritmo ficará assim:
logb x = z.
Calculando o valor de cada logaritmo iremos encontrar duas equações exponenciais:
loga x = y → x = ay
logb x = z → x = bz
Igualando as duas equações teremos:
ay = bz
Assim, podemos montar o seguinte logaritmo:
z = log b ay → utilizando uma das propriedades operatórias dos logaritmos, temos:
z = y . log b a → substituindo z por log b x, temos:
log b x = y . log b a → substituindo y por loga x, temos:
log b x = loga x . log b a → isolando o logaritmo de base a, temos:
loga x = log b x
log b a
Portanto, para transformar loga x em um logaritmo de base b é preciso seguir a seguinte regra:
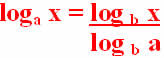
Exemplo 1:
Para transformar log 9 45 em logaritmo na base 10 é preciso seguir a regra estabelecia acima.
Comparando log 9 45 com log a x, podemos dizer que a = 9 e x = 45 e b = 10 (que é a base que queremos transformar) substituindo na
fórmula loga x = log b x, teremos:
log b a
log 9 45 = log 45
log 9
Portanto, log 9 45 na base 10 é log 45, para obter um valor numérico é preciso calcular
log 9
log 45 e log 9.
Exemplo 2:
Esse exemplo é o cálculo de um logaritmo que para ser efetuado será necessário transformar a sua base, veja:
Sabendo que log 2 = 0,3, log 3 = 0,47 e log 5 = 0,69 (todos esses logaritmos estão na base 10), calcule o valor de log2 30.
Para encontrar o valor numérico de log2 30, devemos transformar a base 2 em base 10, pois o exercício ofereceu logaritmos de apoio todos de base 10.
log 2 30 = log 30 = log 5 . 3 . 2 = log 5 + log 3 + log 2 = 0,69 + 0,47 + 0,3 = 1,46 ≈ 4,86
log 2 log 2 log2 0,3 0,3
Portanto, log 2 30 = 4,86.
Por Danielle de Miranda
Graduada em Matemática