As operações com números complexos na forma trigonométrica facilitam o cálculo envolvendo os elementos desse conjunto. Multiplicação e divisão de complexos que estão na forma trigonométrica são feitas quase que instantaneamente, enquanto que na forma algébrica o processo requer mais cálculos. A potenciação e a radiciação de complexos na forma trigonométrica também ficam facilitadas com a utilização das fórmulas de Moivre. Vejamos como se procede a radiciação desses números:
Considere um número complexo qualquer z = a + bi. A forma trigonométrica de z é:
![]()
As raízes de índice n de z são dadas pela segunda fórmula de Moivre:
![]()
Exemplo 1. Determine as raízes quadradas de 2i.
Solução: Primeiro devemos escrever o número complexo na forma trigonométrica.
Todo do número complexo é da forma z = a + bi. Assim, temos que:
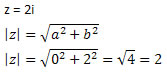
Sabemos também que:
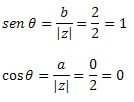
Com os valores de seno e cosseno podemos concluir que:
![]()
Assim, a forma trigonométrica de z = 2i é:
![]()
Agora, vamos calcular as raízes quadradas de z utilizando a fórmula de Moivre.
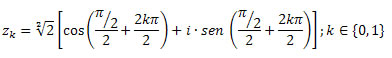
Como queremos as raízes quadradas de z, obteremos duas raízes distintas z0 e z1.
Para k = 0, teremos
![]()
Para k = 1, teremos:
![]()
Ou
![]()
Exemplo 2. Obtenha as raízes cúbicas de z = 1∙(cosπ + i∙senπ)
Solução: Como o número complexo já está na forma trigonométrica, basta utilizar a fórmula de Moivre. Pelo enunciado temos que ø = π e |z| = 1. Assim,
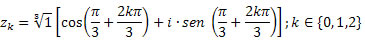
Teremos três raízes distintas, z0, z1 e z2.
Para k = 0
![]()
Para k = 1
![]()
Ou z1 = – 1, pois cos π = – 1 e sen π = 0.
Para k = 2
![]()
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola
