Mediana

A mediana é uma medida de tendência central que divide igualmente um conjunto ordenado de dados. Esse valor se localiza exatamente na posição central da distribuição em rol (organização dos dados em ordem crescente ou decrescente).

Leia também: Média aritmética — como calcular essa outra medida de centralidade

Tópicos deste artigo

• 1 - Resumo sobre mediana
• 2 - Videoaula sobre mediana
• 3 - O que é mediana?
• 4 - Para que serve a mediana?
• 5 - Como calcular a mediana?
• 6 - Média, moda e mediana
• 7 - Exercícios sobre mediana

Resumo sobre mediana

• Mediana é o elemento central em um conjunto de dados ordenado.
• Para calcular a mediana, é importante observar se a quantidade de elementos do conjunto é par ou ímpar.
• Além da mediana, a média e a moda também são medidas de tendência central.

Videoaula sobre mediana

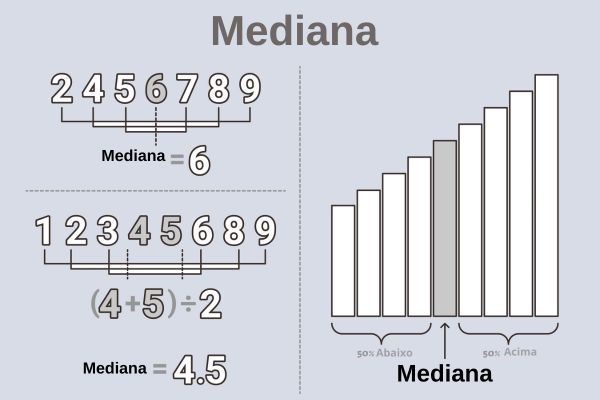
O que é mediana?

A mediana é o termo central de um conjunto ordenado de dados. Isso significa que a mediana divide o conjunto em duas partes com a mesma quantidade de elementos.

Assim como a média e a moda, a mediana é uma das medidas de centralidade da estatística.

Para que serve a mediana?

A mediana é uma medida utilizada para representar o termo central de um conjunto de dados. Essa medida é mais vantajosa que a média quando há muitos valores extremos.

Como calcular a mediana?

O primeiro passo para calcular a mediana de um conjunto de valores é organizar os dados em rol, ou seja, em ordem crescente ou decrescente.

O segundo passo é verificar o número de elementos n  do conjunto:

• Se n  é ímpar, então a mediana é o elemento na posição \(\frac{n+1}{2}\).
• Se n  é par, então a mediana é a média artimética entre os elementos nas posições \(\frac{n}{2} \ e\ \frac{n}{2}+ 1\).

Exemplo 1: Em uma sala de aula há 9 estudantes. Considere o quadro abaixo e determine a mediana das idades dos estudantes dessa sala.

Primeiro organizamos as idades em ordem crescente:

11 11 11 11 12 12 12 13 13

Como o número de elementos do conjunto é igual a 9, que é ímpar, a mediana é o elemento na posição \( \frac{9+1}{2}=5\). O elemento na quinta posição é o primeiro 12 que aparece na distribuição em ordem crescente.

11 11 11 11 12 12 12 13 13

Dessa forma, 12 é a mediana das idades dos estudantes dessa sala.

Note que a mediana divide o conjunto em duas partes, cada uma com 4 elementos.

Exemplo 2: Em uma lanchonete há 6 opções de salgados. Analise o quadro abaixo e determine a mediana dos preços.

Primeiro organizamos os preços em ordem crescente:

3 3 5 6 6 8

Como o número de elementos do conjunto é igual a 6, que é par, a mediana é a média artimética entre os elementos nas posições \(\frac{6}{2}=3\) e \(\frac{6}{2}+1=4\). O elemento na terceira posição é 5 e na quarta posição é o primeiro 6 que aparece na distribuição em ordem crescente.

3 3 5 6 6 8

Assim, a mediana é a média aritmética entre 5 e 6, ou seja, \(\frac{5+6}{2}=\frac{11}{2}=5,5\).

Note que a mediana divide o conjunto em duas partes, cada uma com 3 elementos.

Leia também: Média ponderada — medida central aplicada quando há peso nos dados do conjunto

Média, moda e mediana

A média e moda, assim como a mediana, são medidas de tendência central. Entre os diferentes tipos de média, a mais utilizada é a média aritmética.

• A média aritmética de um conjunto de dados é a razão entre a soma de todos os dados e o número de elementos do conjunto.
• A moda de um conjunto de dados é o elemento que aparece com a maior frequência, ou seja, é o que mais se repete. Se não houver repetição de valores, o conjunto não possui moda.

Exemplo: Calcule a média aritmética, a moda e mediana do seguinte conjunto de dados:

{8, 1, 10, 2, 2, 10, 2}

• Para obter a média aritmética, devemos calcular a divisão entre a soma dos dados e o número 7, pois há 7 elementos no conjunto.

\(Média=\frac{8+1+10+2+2+10+2}{7}=\frac{35}7=5\)

• Para obter a moda, devemos observar qual o elemento que mais se repete no conjunto. Observe que o elemento 2 se repete três vezes, o 10 se repete duas vezes e os demais não se repetem. Assim:

Moda=2  

• Para obter a mediana, devemos organizar os elementos em rol. Vamos ordená-los em ordem crescente:

{1, 2, 2, 2, 8, 10, 10}

Como o número de elementos do conjunto é igual a 7, que é ímpar, a mediana é o elemento na posição \(\frac{7+1}{2}=4.\). O elemento na quarta posição é o último 2 que aparece na distribuição em ordem crescente.

{1, 2, 2, 2, 8, 10, 10}

Assim:

Mediana=2

Para conferir mais exemplos sobre os cálculos de média, moda e mediana, clique aqui.

Exercícios sobre mediana

Questão 1

(Enem) Em uma seletiva para a final dos 100 metros livres de natação, numa olimpíada, os atletas, em suas respectivas raias, obtiveram os seguintes tempos:

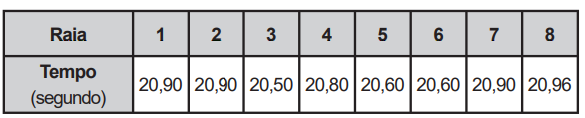
A mediana dos tempos apresentados no quadro é

a) 20,70.

b) 20,77.

c) 20,80.

d) 20,85.

e) 20,90.

Resolução

Organizando os tempos em ordem crescente:

Como são 8 elementos, tem-se que a mediana é a média aritmética entre o quarto e o quinto elemento:

\(\frac{20,80+20,90}{2}=20,85\)

Alternativa D

Questão 2

(Enem) Os candidatos K, L, M, N e P estão disputando uma única vaga de emprego em uma empresa e fizeram provas de português, matemática, direito e informática. A tabela apresenta as notas obtidas pelos cinco candidatos.

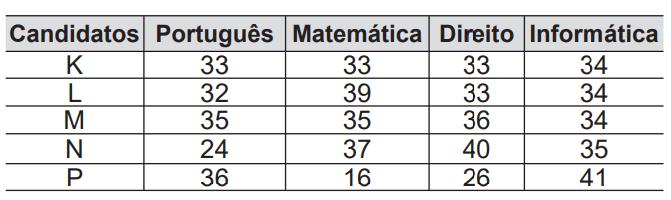
Segundo o edital de seleção, o candidato aprovado será aquele para o qual a mediana das notas obtidas por ele nas quatro disciplinas for a maior. O candidato aprovado será

a) K.

b) L.

c) M.

d) N.

e) P.

Resolução

Como são 4 notas para cada candidato, a mediana será a média aritmética entre o segundo e terceiro termo do conjunto de notas organizado em ordem crescente.

• \(K: \{33,\ \color{red}{33}, \color{red}{33},34\}. A \ mediana \ é \frac{33+33}{2}=33.\)
• \(L: \{34,\ \color{red}{33}, \color{red}{34},39\}. A \ mediana \ é \frac{33+34}{2}=33,5.\)
• \( M: \{34,\ \color{red}{35}, \color{red}{35},36\}. A \ mediana \ é \frac{35+35}{2}=35.\)
• \( N: \{24,\ \color{red}{35}, \color{red}{37},40\}. A \ mediana \ é \frac{35+37}{2}=36.\)
• \( P: \{16,\ \color{red}{26}, \color{red}{41},34\}. A \ mediana \ é \frac{26+41}{2}=33,5.\)

Alternativa D

Fontes:

MAGALHÃES, M. N.; LIMA, A. C. P. de. Noções de Probabilidade e Estatística. 5ª edição. São Paulo: Edusp, 2002.

PIANA, C.F. B.; MACHADO, A. A.; SELAU, L. P. R. Estatística Básica. Departamento de Matemática e Estatística. 2013. (Apostila). Instituto de Física e Matemática, Universidade Federal de Pelotas. Disponível em https://www.ufrgs.br/probabilidade-estatistica/extra/material/apostila_de_estatistica_basica.pdf .