Velocidade de escape, também conhecida como velocidade cósmica primeira, é a mínima rapidez que algum objeto sem propulsão necessita para que possa escapar da atração gravitacional de corpos massivos, como planetas e estrelas. A velocidade de escape é uma grandeza escalar que pode ser calculada quando toda a energia cinética de um corpo é convertida para a forma de energia potencial gravitacional.
Veja também: Cinco descobertas da Física que aconteceram por acidente
Tópicos deste artigo
- 1 - Como se calcula a velocidade de escape?
- 2 - Velocidade orbital ou velocidade cósmica segunda
- 3 - Exercícios resolvidos
Como se calcula a velocidade de escape?
A velocidade de escape é obtida ao assumirmos que toda a energia cinética presente no instante de lançamento de um corpo é transformada em energia potencial gravitacional, para tanto, desconsideramos a ação de forças dissipativas, como o arraste do ar.

Apesar de ser uma velocidade, a velocidade de escape é escalar, uma vez que ela não depende da direção para qual o corpo é lançado: seja um lançamento vertical, ou mesmo na direção tangencial, a rapidez que o corpo precisa estar, de modo que possa escapar do campo gravitacional, é a mesma.
Além de não depender da direção de lançamento, a velocidade de escape tampouco depende da massa do corpo, mas sim da massa do planeta.
A seguir temos o cálculo que é feito para determinar a fórmula da velocidade de escape, para fazê-lo, igualamos a energia cinética com a energia potencial gravitacional, observe:
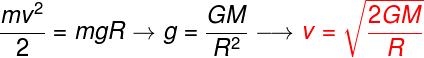
m e M – massa do corpo e do planeta, respectivamente (kg)
g – aceleração da gravidade (m/s²)
G – constante da gravitação universal (6,67.10-11 Nm²/kg²)
R – distância em relação ao centro do planeta (m)
v – velocidade de escape (m/s)
O cálculo mostrado levou em conta a fórmula da gravidade, dada pela razão entre a massa do planeta e o quadrado de seu raio médio, multiplicada pela constante gravitacional. O resultado obtido mostra que a velocidade de escape depende tão somente do raio e da massa do planeta, portanto, vamos calcular qual é a velocidade de escape de um corpo que é projetado a partir da superfície da Terra, no nível do mar:
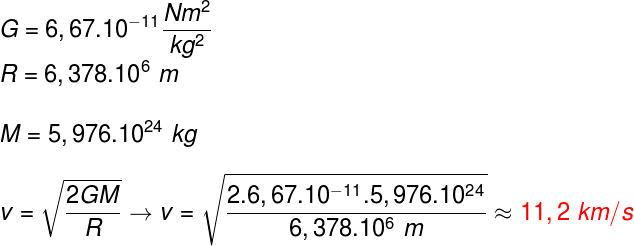
O cálculo apresentado mostra que se um objeto for lançado a partir da superfície da Terra, com velocidade mínima de 11,2 km/s, na ausência de forças dissipativas, esse corpo escapará da órbita terrestre.
Veja também: O que são os buracos negros e o que sabemos sobre eles?
Velocidade orbital ou velocidade cósmica segunda
Velocidade orbital, também conhecida como velocidade cósmica segunda, é a velocidade com a qual algum objeto em órbita move-se ao redor de seu astro. A velocidade orbital é sempre tangente à trajetória do corpo em órbita, para calculá-la, dizemos que a força de atração gravitacional é equivalente à força centrípeta, que mantém o corpo em movimento circular ou em uma trajetória elíptica, por exemplo.
A seguir, mostramos a fórmula que é utilizada para o cálculo da velocidade orbital, observe:
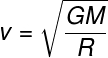
A fórmula leva em conta a massa do astro em que um corpo orbita, bem como o raio de sua órbita, medido a partir do centro desse astro. A partir dessa fórmula e daquela que é usada para calcular a velocidade de escape, é possível estabelecer uma relação entre essas duas velocidades, essa relação é mostrada abaixo:
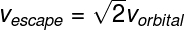
Exercícios resolvidos
Questão 1) (Uem) Em um livro do escritor estadunidense de ficção científica Robert Anson Heinlein (1907-1988), lê-se: “A escolha do pessoal para a primeira expedição humana a Marte foi feita tendo como base a teoria de que o maior perigo para o homem era o próprio homem. Naquele tempo – oito anos terrestres depois da fundação da primeira colônia humana em Luna – uma viagem interplanetária de seres humanos devia ser feita em órbitas de queda livre, levando, da Terra a Marte, cento e cinquenta e oito dias terrestres e vice-versa, além de uma espera em Marte de cento e cinquenta e cinco dias, até que os planetas voltassem lentamente às posições anteriores, permitindo a existência de uma órbita de retorno.” (adaptado)
(HEINLEIN, R. A. Um estranho numa terra estranha. Rio de Janeiro: Artenova, 1973, p. 3).
Considere a razão entre as massas da Terra e de Marte igual a 9 e a razão entre os raios da Terra e de Marte igual a 2 considere, ainda, que não há forças de atrito e que a velocidade de escape de um corpo é a velocidade mínima com que se deve lançá-lo a partir da superfície de um astro para que ele consiga vencer a atração gravitacional desse astro.
Assinale o que for correto.
01) A velocidade de escape de um corpo é diretamente proporcional à raiz quadrada da razão entre a massa e o raio do planeta.
02) A velocidade de escape de uma espaçonave a partir da superfície da Terra é menor do que a velocidade de escape com que se deve lançar a mesma espaçonave a partir da superfície de Marte.
04) A velocidade de escape de uma espaçonave não depende de sua massa.
08) Para que uma espaçonave orbite o planeta Marte, a velocidade dela deve ser proporcional ao raio da órbita.
16) Uma espaçonave com os motores desligados e aproximando-se de Marte está sujeita a uma força que depende de sua velocidade.
A soma das alternativas corretas é igual a:
a) 12
b) 3
c) 5
d) 19
e) 10
Solução
Alternativa C.
Vamos analisar cada uma das alternativas:
01 – VERDADEIRO – A fórmula da velocidade de escape depende da raiz quadrada da massa do planeta pelo seu raio.
02 – FALSO – Para verificarmos isso é necessário que utilizemos a fórmula da velocidade de escape, levando em conta que a massa da Terra é 9 vezes maior que a massa de Marte e que o raio da Terra é 2 vezes maior que o raio de Marte:
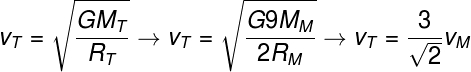
De acordo com a resolução, a velocidade de escape da Terra é maior que a velocidade de escape em Marte, portanto, a afirmativa é falsa.
04 – VERDADEIRO – Basta analisarmos a fórmula da velocidade de escape para constatarmos que ela só depende da massa do planeta.
08 – FALSO – A velocidade orbital precisa ser inversamente proporcional à raiz quadrada do raio orbital.
16 – FALSO – A força que atrai a espaçonave até Marte é gravitacional e seu módulo pode ser calculada segundo a Lei da gravitação universal. De acordo com tal lei, a atração gravitacional é proporcional ao produto das massas e inversamente proporcional ao quadrado das distâncias, nada sobre a grandeza velocidade é mencionado nessa lei, portanto, a alternativa é falsa.
A soma das alternativas é igual a 5.
Questão 2) (Cefet MG) Um foguete é lançado de um planeta de massa M e raio R. A velocidade mínima necessária para que ele escape da atração gravitacional e vá para o espaço é dada por:
a)
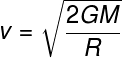
b)
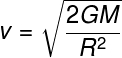
c)
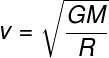
d)
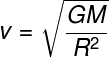
e)
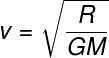
Solução
Alternativa C.
A fórmula usada para calcular a velocidade de escape é a mostrada na letra C, como explicado no artigo.
Por Rafael Helerbrock
Professor de Física
