Movimento circular é o movimento de rotação de um corpo em torno de um eixo ao longo de uma trajetória circular de raio constante. Esse movimento pode ser uniforme, caso a velocidade de rotação seja constante, ou variado, caso sua velocidade sofra variações ao longo do tempo.
Tópicos deste artigo
- 1 - Introdução ao movimento circular
- 2 - Mapa Mental: Movimento Cicular Uniforme
- 3 - Movimento circular uniforme (MCU)
- 4 - Força centrípeta no MCU e no MCUV
- 5 - Movimento circular uniformemente variado (MCUV)
- 6 - Fórmulas do Movimento Circular
- 7 - Exemplos de movimento circular
Introdução ao movimento circular
O movimento circular ocorre quando uma força de módulo constante é aplicada em uma direção perpendicular à velocidade de um móvel, de forma que o módulo dessa velocidade mantenha-se constante, alterando somente sua direção e seu sentido. A força aplicada nesse caso é denominada força centrípeta.
Para que seja melhor entendido, o movimento circular é dividido em duas partes: a parte angular e a parte espacial. Enquanto o móvel desloca-se no espaço, o ângulo formado em relação ao seu eixo de rotação também varia. Por isso, ao tratarmos do movimento circular, falamos de conceitos como deslocamento angular e velocidade angular.
Observe a figura abaixo:
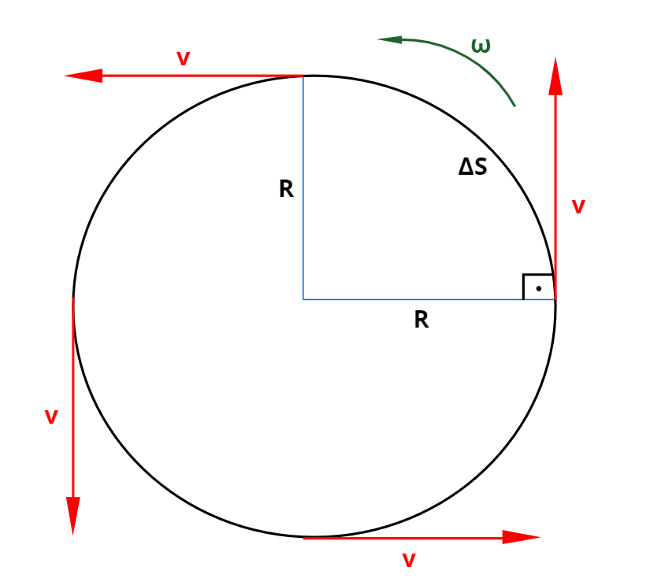
No movimento circular, a velocidade escalar (v) é perpendicular ao raio da trajetória (R) e é tangente ao deslocamento (ΔS).
A figura acima mostra a trajetória de um móvel que executa um movimento circular uniforme, ou seja, com velocidade tangencial (v) constante. Caso sua velocidade apresente aceleração ou desaceleração constante, o movimento executado por esse corpo é circular uniformemente variado.
Mapa Mental: Movimento Cicular Uniforme
.jpeg)
*Baixe o mapa mental movimento circular uniforme!
Movimento circular uniforme (MCU)
No movimento circular uniforme (MCU), a velocidade tangencial com a qual o móvel desloca-se permanece constante e pode ser escrita como a divisão entre o deslocamento (ΔS) e o intervalo de tempo do movimento (Δt):
![]()
v – velocidade média
ΔS – deslocamento
Δt – intervalo de tempo
O deslocamento (ΔS) sofrido pelo móvel é dado pelo comprimento da circunferência de raio R e é calculado por meio da expressão:
![]()
Além disso, chamamos de período (T) o tempo necessário para que o móvel complete uma volta em torno de seu eixo de rotação. Podemos, assim, reescrever a equação da velocidade para o MCU da seguinte forma:
![]()
R – raio da circunferência
T – período
Chamamos de velocidade angular (ω) a variação do ângulo θ formado entre o raio e seus eixos horizontal e vertical. Observe a figura abaixo:
.jpg)
ω – velocidade angular
A velocidade angular média pode ser calculada, portanto, por meio do deslocamento angular de uma volta completa (2π em radianos) divido pelo período (T) dessa volta. Além disso, devemos lembrar que período (T) e frequência (f) de rotação são grandezas inversas. Há, portanto, mais de uma forma de calcularmos a velocidade angular de um movimento circular:
![]()
f - frequência
De acordo com o Sistema Internacional de Unidades (SI), a unidade utilizada para calcularmos a velocidade angular é o radianos por segundo (rad/s). Lembre-se:
-
1 radiano é o ângulo cujo arco (ΔS) tem comprimento igual ao raio (R) da sua circunferência.
-
Uma volta completa em torno de uma circunferência equivale a 360º ou 2π radianos.
Veja também: O que determina o sentido com o qual a água desce pelo ralo?
Caso saibamos a frequência de rotação de um móvel e queiramos determinar seu período, ou vice-versa, podemos usar a identidade apresentada abaixo:
![]()
A frequência é o inverso do período, e vice-versa.
A unidade de frequência no SI é o hertz (Hz), que é equivalente à unidade s-1 (unidade que mede a quantidade de oscilações ou rotações completadas a cada segundo). Outra unidade comumente usada para frequência é o rpm (rotações por minuto). Para convertermos essas unidades basta lembrarmos que 1 Hz = 60 rpm.
Veja também: Transmissão de movimento circular
Velocidade escalar no MCU
É possível relacionar velocidade escalar (ou tangencial) e velocidade angular de um móvel que executa um MCU por meio da seguinte fórmula:
![]()
A fórmula acima permite relacionar a velocidade escalar à velocidade angular de um móvel que executa um MCU.
Resumo sobre MCU
Confira abaixo um quadro-resumo que pode nos ajudar a entender o MCU:
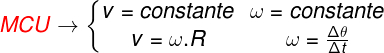
Força centrípeta no MCU e no MCUV
Força centrípeta é toda força central (que aponta para o centro) que age em direção perpendicular à velocidade de um móvel, mudando, assim, sua direção e seu sentido sem alterar o módulo de sua velocidade. A força centrípeta pode ser calculada por meio da expressão abaixo:
![]()
FCP – força centrípeta
m – massa do móvel
v – velocidade escalar do móvel
R – raio da trajetória do móvel
Veja também: O que é força centrífuga?
É importante lembrar que, mesmo que um corpo mova-se em movimento circular uniforme (MCU), seu movimento será acelerado. Nesse caso, a aceleração que o corpo sofre é centrípeta e aponta sempre para o centro de sua trajetória, na direção de seu raio.
A aceleração centrípeta pode ser calculada por meio da fórmula abaixo:
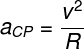
ACP – aceleração centrípeta
v – velocidade
R – raio da trajetória
Quando o corpo em movimento circular apresenta alguma outra aceleração constante além da centrípeta, dizemos que seu movimento é circular e uniformemente variado (MCUV), como no caso da figura abaixo:
.jpg)
AT – aceleração tangencial
AC – aceleração centrípeta
Nessa figura, podemos ver que o móvel apresenta uma aceleração centrípeta (perpendicular à velocidade) e uma aceleração tangencial (paralela à velocidade). Logo, o móvel está acelerando sua rotação.
Nesse caso, é possível calcularmos a aceleração resultante por meio do Teorema de Pitágoras, uma vez que as acelerações centrípeta e tangencial são perpendiculares entre si:
![]()
Movimento circular uniformemente variado (MCUV)
O MCUV é um movimento circular que ocorre quando a velocidade angular do móvel varia de forma constante com o tempo. Isso significa que a rotação ocorre na presença de uma aceleração angular.
As equações utilizadas para descrever o MCUV são similares àquelas utilizadas no movimento uniformemente variado (MUV). Para determinarmos, por exemplo, a velocidade angular final após uma aceleração ou desaceleração angular, utilizamos a fórmula abaixo:
![]()
ω – velocidade angular final
ω0 – velocidade angular inicial
α – aceleração angular
A aceleração angular, por sua vez, pode ser calculada por meio da seguinte fórmula:
![]()
Δω – variação da velocidade angular
O deslocamento angular do móvel é a medida da variação do ângulo θ, em radianos, para uma dada velocidade angular inicial (ω0) e para uma determinada aceleração angular (α). O deslocamento angular pode ser calculado por meio da equação abaixo:
![]()
Δθ – deslocamento angular
Resumo sobre MCUV
Confira abaixo um quadro-resumo com a síntese das ideias relacionadas ao movimento circular uniformemente variado:
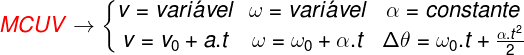
Fórmulas do Movimento Circular
Confira um resumo das principais fórmulas utilizadas para o estudo do MCU e do MCUV:
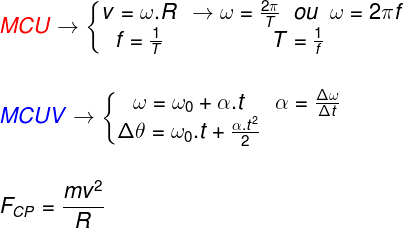
Exemplos de movimento circular
→ MCU
Uma roda gigante com 10 m de diâmetro gira a uma frequência de 15 rpm. Determine:
a) a frequência dessa roda gigante em Hz.
b) o período de oscilação dessa roda gigante.
c) sua velocidade angular.
d) a velocidade escalar das extremidades da roda gigante.
e) o espaço percorrido por uma pessoa sentada na extremidade da roda gigante durante uma volta completa.
Resolução
a) Para determinarmos a frequência dessa roda gigante em Hz, basta lembrarmos que 1 minuto tem 60 segundos. Com isso, dividimos sua frequência de 15 rpm por 60 s, resultando 0,25 Hz.
f = 0,25 Hz
b) O período da oscilação é dado pelo inverso da frequência da roda gigante. Nesse caso, teremos 1 dividido por 0,25, resultando em 4 segundos.
![]()
T = 4 s
c) Podemos calcular a velocidade angular da roda gigante usando uma das equações abaixo:
![]()
Usando a primeira opção, teremos o seguinte cálculo:
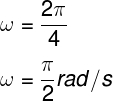
d) A velocidade escalar da roda gigante depende da distância do ponto em que se deseja calcular a velocidade até o eixo de rotação desse corpo. De acordo com o enunciado do exercício, o diâmetro dessa roda gigante é de 10 m, e a medida de seu raio é de 5 m:
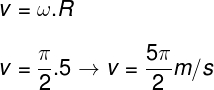
e) Podemos calcular o espaço percorrido por um ponto que se encontra na extremidade da roda gigante durante uma volta completa. Para isso, basta multiplicarmos a velocidade da roda gigante pelo período:
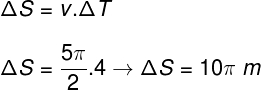
→ MCUV
Um ponto material move-se em MCUV com velocidade angular inicial de 0,5 rad/s e, então, passa a acelerar a 0,5 rad/s² durante 1,0 s. Sendo o raio de sua trajetória igual a 5,0 m, determine:
a) a velocidade angular desse ponto material ao final do tempo de 1,0 s.
b) o deslocamento angular sofrido por esse ponto material durante o tempo de 1,0 s.
c) o deslocamento escalar sofrido pelo ponto material.
Resolução
a) A velocidade angular final do móvel pode ser calculada por meio da fórmula abaixo:
![]()
Considerando os dados fornecidos pelo enunciado do exercício, teremos a seguinte resolução:
![]()
b) Para determinarmos o deslocamento angular sofrido por esse móvel, usaremos a equação:
![]()
Usando as informações do exercício, faremos o seguinte cálculo:
![]()
c) Por fim, para calcularmos a distância percorrida pelos pontos extremos da roda gigante, basta usarmos a equação abaixo:
![]()
Multiplicando o deslocamento angular de 0,75 rad pelo raio da roda gigante de 5m, teremos um deslocamento escalar de 3,75 m, equivalente a uma volta completa.
Por Me. Rafael Helerbrock
