O que é velocidade média?

Velocidade média é a variação da posição (deslocamento) de um móvel em relação a um referencial durante certo intervalo de tempo. A unidade de medida da velocidade média, de acordo com o SI, é o metro por segundo (m/s).

Veja também: Movimento uniformemente variado (MUV) – resumo e exercícios

Tópicos deste artigo

• 1 - O que é velocidade média?
• 2 - Cálculo da velocidade média
• 3 - Velocidade média e velocidade escalar média
• 4 - Velocidade média vetorial
• 5 - Exercícios resolvidos sobre velocidade média

O que é velocidade média?

A velocidade média é uma grandeza vetorial que depende das diferenças entre as posições final e inicial de um movimento. Durante uma corrida de Fórmula 1, por exemplo, os carros podem desenvolver altíssimas velocidades instantâneas, no entanto, ao final da corrida, terão voltado à posição inicial. Desse modo, sua velocidade média durante todo o percurso foi igual a zero.

Uma vez que a velocidade média depende exclusivamente da diferença entre as posições, não importa se um corpo permaneceu parado a maior parte do tempo ou se ele acelerou, por exemplo. Quer aprender mais? Confira o nosso texto sobre o movimento uniforme.

A seguir, apresentamos a fórmula usada para o cálculo da velocidade média, observe:

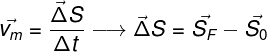
v_m – velocidade média (m/s)

ΔS – deslocamento (m/s)

S_F – posição final (m)

S0 posição inicial (m)₀S

Um detalhe importante sobre a velocidade média é que ela não pode ser confundida com a média das velocidades. Isso só é possível quando o tempo gasto em cada parte do trajeto for igual para cada uma das velocidades. Esse tipo de média é chamada: média harmônica.

Cálculo da velocidade média

Graficamente podemos entender a velocidade média como a inclinação da reta da posição em função do tempo, quanto mais inclinada for essa reta, maior é a sua velocidade média. Nesse sentido compreendemos que a velocidade média é medida pelo coeficiente angular da reta.

Observe o gráfico seguinte que relaciona a posição x com o tempo:

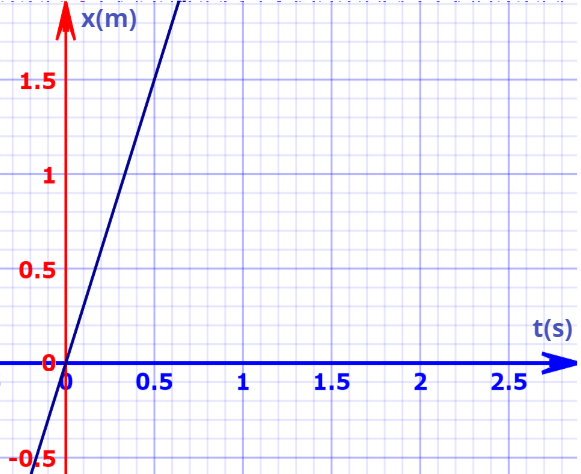
Se quisermos calcular a velocidade média do movimento ilustrado pelo gráfico, é necessário calcularmos o seu coeficiente angular. Para tanto vamos escolher os pontos de t = 0 s e t = 0,5 s, respectivos às posições x(t) = 0 m e x(t) = 1,5 m, como mostrado a seguir:

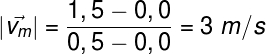
Por meio da aplicação da fórmula da velocidade média, descobrimos que esse móvel desloca-se, na média, três metros a cada segundo. Adiante colocamos em um gráfico a posição em função do tempo para dois móveis diferentes, sendo que um desses (em amarelo) é acelerado:

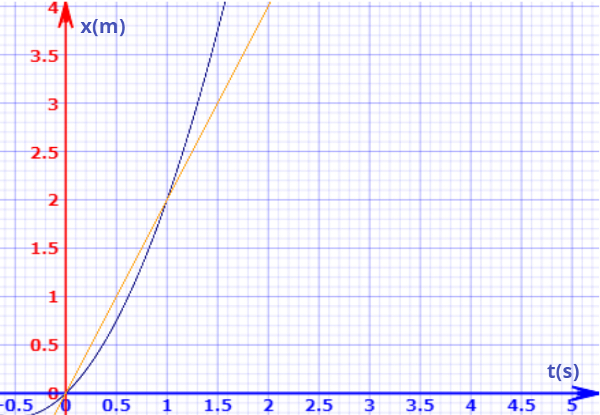
Observe que, entre os instantes de tempo t = 0,0 s e t = 1,0 s, os dois móveis percorreram a mesma distância: x = 2,0 m. Assim, durante esse intervalo de tempo, apesar de tratarem-se de movimentos diferentes, os móveis retratados tiveram a mesma velocidade média, no entanto, isso não é mais verdade para instantes de tempo maiores que t = 1,0 s.

Por tratar-se de uma grandeza vetorial, o deslocamento deve ser calculado como tal, levando em conta a diferença entre as posições final e inicial, nas três direções do espaço. No entanto, em alguns casos, como aqueles frequentemente apresentados nos livros de Ensino Médio, leva-se em conta apenas uma direção do movimento, de modo que é necessário somente que se subtraiam os módulos das posições S_F e S₀. Confira um exemplo de exercício resolvido sobre velocidade média ao longo de uma reta:

Exemplo – Um automóvel parte de uma cidade localizada às margens do quilômetro 640 de uma rodovia retilínea. Duas horas depois, encontra-se no quilômetro 860 dessa mesma rodovia. Determine a velocidade média desse automóvel.

Resolução:

Para calcular a velocidade média, basta assumirmos que o deslocamento do automóvel é igual ao espaço total por ele percorrido: 220 km. Em seguida, basta fazermos a divisão entre essa distância e o tempo necessário para percorrê-la:

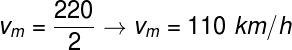
Assim como essa situação, existem diversos exercícios nos livros didáticos em que se desconsidera a direção e o sentido do movimento, por isso, fala-se em velocidade escalar média, um conceito físico pouco coerente, uma vez que toda velocidade é vetorial. Nesse caso, o que deve ser entendido é que esses exercícios referem-se ao módulo ou magnitude da velocidade.

Essa velocidade escalar média é, por sua vez, definida pelo espaço total percorrido dividido pelo intervalo de tempo. Falaremos um pouco mais sobre as diferenças entre a velocidade média e a velocidade escalar média adiante.

Velocidade média e velocidade escalar média

A velocidade escalar média é usada para definir a rapidez com que um móvel desloca-se, sem levar em conta a direção e o sentido de seu movimento. Portanto, essa velocidade é um caso particular da velocidade média, em que o móvel desloca-se sempre na mesma direção e no mesmo sentido.

O significado de velocidade media, por sua vez, é muito mais amplo, e pode referir-se ao movimento de um corpo nas três direções do espaço, por exemplo.

Agora apresentamos a fórmula usada para o cálculo da velocidade escalar média:

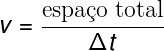
Vamos conferir um exemplo de uso dessa fórmula:

Exemplo – Um viajante deseja completar um trajeto de 120 km com velocidade média de 60 km/h. Sabendo que o viajante percorreu três quartos do trajeto à velocidade de 50 km/h, em quanto tempo ele deverá percorrer o restante do trajeto de modo a conseguir completá-lo de acordo com a velocidade média que ele havia planejado?

Resolução:

De acordo com o exercício, o viajante deseja completar a sua viagem com velocidade média de 60 km/m. Sabendo-se que o trajeto a ser percorrido é de 120 km, conclui-se que a duração de sua viagem deve ser de 2 h.

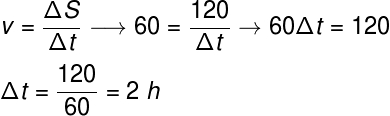
De acordo com o enunciado, o viajante percorreu três quartos (¾) do trajeto de 120 km (ou seja, 90 km) a uma velocidade de 50 km/h. Nesse caso vamos calcular o tempo gasto para esse trajeto da viagem.

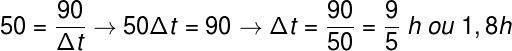
O resultado obtido indica que restam apenas 0,2 h para completar o trajeto, uma vez que o tempo total deve ser de 2,0 h. Além disso, como 1 h tem 60 minutos, o viajante deverá finalizar a sua viagem, no máximo, em 12 minutos.

Caso o exercício solicite, também é possível calcular qual é a velocidade média que o viajante deve desenvolver no trajeto restante, para isso, basta dividirmos o espaço que ele ainda não percorreu pelo tempo restante, veja como:

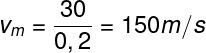
O resultado obtido indica que, para completar o trajeto de acordo com a velocidade média planejada, o viajante deverá mover-se a uma velocidade de 150 km/h.

Veja também: Descubra o que você deve estudar sobre Mecânica para a prova do Enem

Velocidade média vetorial

A velocidade vetorial média deve ser calculada de acordo com as regras da soma vetorial.

Na figura mostramos as posições (x₀,y₀) e (x_F,y_F) de um móvel em relação ao referencial (0,0):

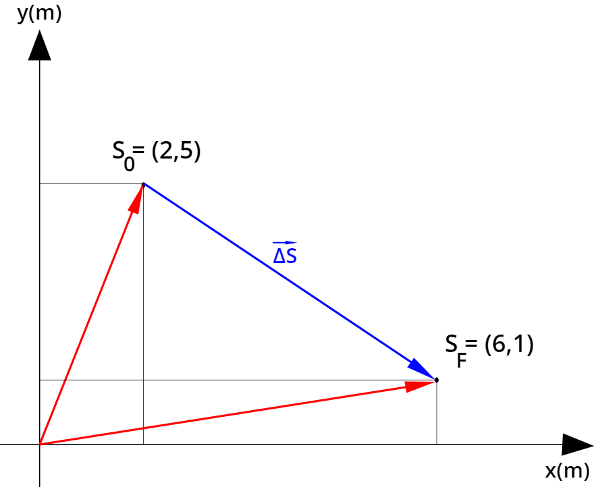
Na figura observa-se um movimento bidimensional, no qual um móvel parte da posição S₀ (2, 5) e desloca-se até a posição S_F (6, 1), desse modo, o seu deslocamento, ou seja, a diferença entre as posições final e inicial, foi (4, -4). As setas vermelhas são os vetores de posição, que localizam o objeto em relação ao referencial (0,0).

Vamos supor que esse deslocamento tenha ocorrido em um intervalo de tempo igual a 2,0 segundos, nesse caso, para calcularmos o módulo da velocidade vetorial média, é necessário determinar o módulo do vetor deslocamento, que pode ser obtido pelo teorema de Pitágoras, uma vez que as direções x e y são perpendiculares entre si:

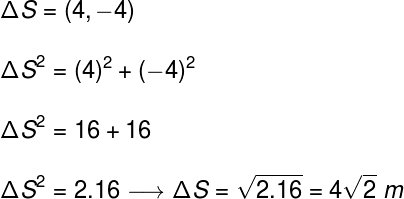
Após determinarmos o módulo do deslocamento, basta utilizarmos a fórmula da velocidade média, dividindo o resultado pelo intervalo de tempo em que o movimento ocorreu:

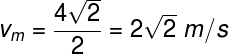
Exercícios resolvidos sobre velocidade média

Questão 1) Um carro de Fórmula 1 percorre uma pista circular de 1,0 km de comprimento, levando 20 segundos para completar uma volta, depois de ter partido da largada, que também marca o final de uma volta. A alternativa que apresenta corretamente o módulo da velocidade média desse veículo ao longo de uma volta completa é:

a) 50 m/s

b) 0 m/s

c) 180 m/s

d) 20 m/s

e) 45 m/s

Gabarito: Letra b

Resolução:

Para resolver esse exercício, basta lembrarmo-nos de que a velocidade média é vetorial e depende diretamente do deslocamento, que, nesse caso, é igual a zero, uma vez que, tendo completado uma volta, o automóvel encontra-se na mesma posição da qual havia partido, logo, sua velocidade média é igual a zero.

Questão 2) Para deixar uma encomenda, um entregador desloca-se duas quadras ao norte e três quadras a leste, em um intervalo de tempo de 15 minutos. Desprezando-se o comprimento das ruas e levando-se em conta que o comprimento de cada quadra é de 50 m, determine a velocidade média e a velocidade escalar média, em km/h, desenvolvidas pelo carteiro.

a) 0,7 km/h e 3,6 km/h

b) 2,5 km/h e 4,0 km/h

c) 5,0 km/h e 4,0 km/h

d) 2,0 km/h e 1,0 km/h

e) 0,9 km/g e 2,7 km/h

Gabarito: Letra a

Resolução:

De acordo com o exercício, o entregador desloca-se três quadras a leste e duas quadras ao norte, sendo que o comprimento de cada uma dessas quadras é de 50 m. Desse modo, sabemos que o espaço total percorrido pelo entregador é de 250 m (0,25 km), pois ele passou por cinco quadras diferentes.

Com as informações até então obtidas, como o espaço total percorrido (250 m) e o tempo de translado (15 minutos = 0,25 h), é fácil calcular sua velocidade escalar média:

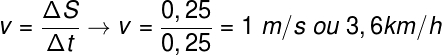
A velocidade vetorial média, por sua vez, é um pouco mais complexa. Para podermos calculá-la, é necessário determinar qual foi o deslocamento vetorial do carteiro. Nesse caso sabemos que o carteiro moveu-se 150 m na direção horizontal (rumo ao leste) e 100 m na direção vertical (rumo ao norte). Para obtermos seu deslocamento, é necessário aplicarmos o teorema de Pitágoras, observe:

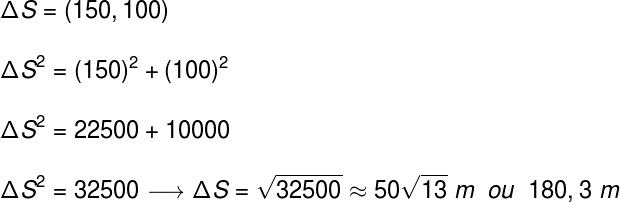
Por fim, para descobrirmos a velocidade desse entregador, dividimos a distância percorrida pelo tempo total em segundos:

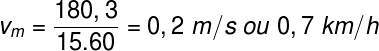
Reunindo as informações obtidas, temos que a velocidade média vetorial do entregador é de 0,7 km/h, enquanto a sua velocidade escalar média é de 3,6 km/h.