Teorema de Stevin

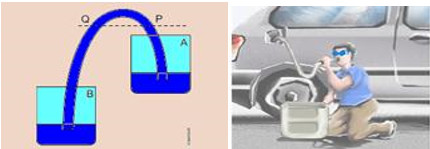
O teorema de Stevin é a lei que afirma que a variação de pressão entre dois pontos de um fluido é determinada pelo produto entre a densidade do fluido, aceleração da gravidade e variação de altura entre esses pontos. Por meio do teorema de Stevin foi possível formular o teorema de Pascal e o princípio dos vasos comunicantes.

Leia também: Empuxo — a força que surge quando algum corpo é inserido no interior de um fluido

Tópicos deste artigo

• 1 - Resumo sobre teorema de Stevin
• 2 - O que diz o teorema de Stevin?
• 3 - Fórmula do teorema de Stevin
• 4 - Consequências e aplicações do teorema de Stevin
  • → Princípio dos vasos comunicantes
  • → Teorema de Pascal
• 5 - Unidades de medida do teorema de Stevin
• 6 - Exercícios resolvidos sobre teorema de Stevin

Resumo sobre teorema de Stevin

• O teorema de Stevin é a lei fundamental da hidrostática e foi desenvolvido pelo cientista Simon Stevin.

• De acordo com o teorema de Stevin, quanto mais próximo ao nível do mar um corpo estiver, menor será a pressão sobre ele.

• As principais aplicações do teorema de Stevin são os vasos comunicantes e o teorema de Pascal.

• Nos vasos comunicantes, a altura dos líquidos é a mesma independentemente do formato do vaso, só alterando se os líquidos colocados possuírem diferentes densidades.

• O teorema de Pascal afirma que a pressão sofrida em um ponto de um líquido será transferida para o restante dele, considerando que todos sofreram com a mesma variação de pressão.

O que diz o teorema de Stevin?

Também conhecido como a lei fundamental da hidrostática, o teorema de Stevin foi formulado pelo cientista Simon Stevin (1548-1620). Ele é enunciado da seguinte forma:

A diferença de pressão entre os dois pontos de um líquido homogêneo em equilíbrio é constante, dependendo apenas do desnível entre esses pontos.|1|

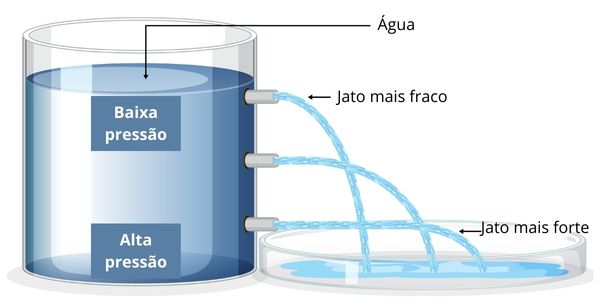
Ele trata da variação de pressão atmosférica e hidráulica (nos líquidos) a diferentes alturas ou profundidades. Assim, quanto mais na superfície ou no nível do mar estiver um corpo, menor será a pressão sofrida sobre ele. Porém, à medida que essa diferença aumenta, maior é a pressão sobre o corpo, como podemos ver na imagem a seguir:

Fórmula do teorema de Stevin

\(∆p=d\cdot g\cdot∆h\) ou \(p-p_o=d\cdot g\cdot∆h\)

• \(∆p\) → pressão manométrica ou variação de pressão, medida em Pascal \([Pa]\).

• p → pressão absoluta ou total, medida em Pascal \([Pa]\).

• \(p_o\) → pressão atmosférica, medida em Pascal \([Pa]\).

• d → densidade ou massa específica do fluido, medida em \([kg/m^3]\).

• g → gravidade, medida em \([m/s^2]\).

• \(∆h\) → variação de altura, medida em metros \([m]\).

Consequências e aplicações do teorema de Stevin

O teorema de Stevin é aplicado em diversas situações do cotidiano, tais como o sistema hidraúlico das casas e o local adequado para instalação de caixas d’água. Além disso, sua formulação possibilitou o desenvolvimento do princípio dos vasos comunicantes e o teorema de Pascal.

→ Princípio dos vasos comunicantes

O princípio dos vasos comunicantes afirma que em um recipiente composto por ramificações que se interligam, ao despejar um líquido de mesma densidade sobre as ramificações, ele terá o mesmo nível e sofrerá a mesma pressão em qualquer uma das partes. A seguir, podemos ver como são os vasos comunicantes:

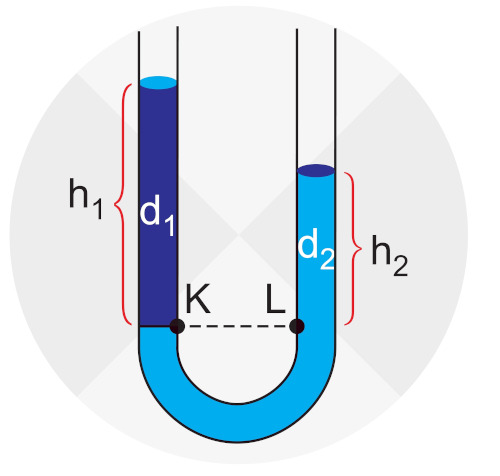
Caso sejam colocados liquídos com diferentes densidades em um recipiente no formato de U, as alturas dos líquidos e pressões exercidas sobre eles serão diferentes, como podemos ver na imagem a seguir:

◦ Fórmula do princípio dos vasos comunicantes

O princípio dos vasos comunicantes pode ser calculado por meio da sua fórmula:

\(\frac{H_1}{H_2} =\frac{d_2}{d_1} \) ou H1∙d1=H2∙d2

• \(H_1\) e \(H_2\) → alturas relacionadas às áreas, medidas em metros \([m]\).

• \(d_1\) e \(d_2\) → densidades dos fluidos, medidas em \([kg/m^3]\).

Esse princípio permite que os vasos sanitários contenham o mesmo nível de água e que seja possível medir a pressão e densidade dos fluidos nos laboratórios.

→ Teorema de Pascal

Formulado pelo cientista Blaise Pascal (1623-1662), o teorema de Pascal afirma que ao aplicar uma pressão em um ponto de um líquido em equilíbrio, essa variação propagará para o restante do líquido, fazendo com que todos os seus pontos sofram com a mesma variação de pressão.

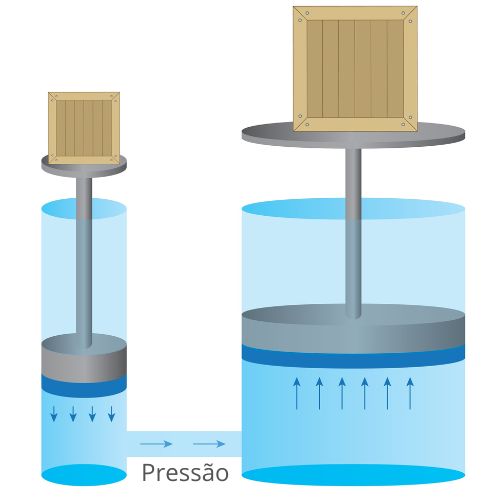
Por meio desse teorema, foi desenvolvida a prensa hidráulica. Se aplicarmos uma força para baixo sobre um pistão, haverá um aumento de pressão que ocasionará o deslocamento do fluido para o outro pistão, causando sua elevação, como podemos ver na imagem a seguir:

◦ Fórmula do teorema de Pascal

O teorema de Pascal pode ser calculado por meio da sua fórmula:

\(\frac{\vec{F}_1}{A_1} =\frac{\vec{F}_2}{A_2} \) ou \(\frac{A_1}{A_2} =\frac{H_2}{H_1} \)

• \(\vec{F}_1\) e \(\vec{F}_2\) → forças aplicada e recebida, respectivamente, medidas em Newton \([N]\).

• \(A_1\) e \(A_2\) → áreas relacionadas à aplicação das forças, medidas em \([m^2]\).

• \(H_1\) e \(H_2\) → alturas relacionadas às áreas, medidas em metros \([m]\).

Unidades de medida do teorema de Stevin

Diversas unidades de medida são empregadas no teorema de Stevin. A seguir, veremos uma tabela com as unidades de medidas de acordo com o Sistema Internacional de Unidades (S.I.), outra forma comum em que elas aparecem e como converter uma na outra.

Veja também: Força peso — a força atrativa existente entre dois corpos

Exercícios resolvidos sobre teorema de Stevin

Questão 1

(Unesp) A diferença de pressão máxima que o pulmão de um ser humano pode gerar por inspiração é em torno de \(0,1\cdot10^5\ Pa\) ou \(0,1\ atm\). Assim, mesmo com a ajuda de um snorkel (respiradouro), um mergulhador não pode ultrapassar uma profundidade máxima, já que a pressão sobre os pulmões aumenta à medida que ele mergulha mais fundo, impedindo-os de inflarem.

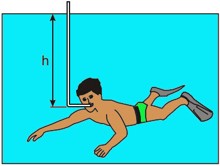
Considerando a densidade da água \(10^3\ kg/m\) e a aceleração da gravidade \(10\ m/s^2\), a profundidade máxima estimada, representada por h, que uma pessoa pode mergulhar respirando com a ajuda de um snorkel é igual a

A) 1,1 ‧ 10² m

B) 1,0 ‧ 10² m

C) 1,1 ‧ 10¹ m

D) 1,0 ‧ 10¹ m

E) 1,0 ‧ 10⁰ m

Resolução:

Alternativa E

A diferença de pressão (Δp) pode ser dada pela lei de Stevin:

\(∆p=d\cdot g\cdot ∆h\)

\(0,1\cdot10^5=10^3\cdot10\cdot∆h\)

\(0,1\cdot10^5=10^4\cdot∆h\)

\(∆h=\frac{0,1\cdot10^5}{10^4} \)

\(∆h=0,1\cdot10^{5-4}\)

\(∆h=0,1\cdot10^1\)

\(∆h=1\cdot10^0\ m\)

Questão 2

(Aman) Um tanque contendo \(5,0\ x\ 10^3\) litros de água tem 2,0 metros de comprimento e 1,0 metro de largura. Sendo \(g=10\ m/s^2\),  a pressão hidrostática exercida pela água no fundo do tanque vale:

A) \(2,5\cdot10^4\ Nm^{-2}\)

B) \(2,5\cdot10^1\ Nm^{-2}\)

C) \(5,0\cdot10^3\ Nm^{-2}\)

D) \(5,0\cdot10^4\ Nm^{-2}\)

E) \(2,5\cdot10^6\ Nm^{-2}\)

Resolução:

Alternativa A

É necessário modificar a unidade de medida do volume de litros para \(m^3\):

\(V=5\cdot10^3\ L=5\ m^3\)

A altura será dada por:

\(5=1\cdot2\cdot h\)

\(5=2\cdot h\)

\(\frac{5}2=h\)

\(2,5=h\)

Calcularemos a pressão hidrostática exercida pela água no fundo do tanque usando o teorema de Stevin:

\(p=d\cdot g\cdot h\)

Considerando a densidade da água como \(1000\ kg/m^3 \) e a gravidade como \(10\ m/s^2\), encontramos:

\(p=1000\cdot10\cdot2,5\)

\(p=2,5\cdot10^4\ Pa=2,5\cdot10^4\ Nm^{-2}\)

Notas

|1| NUSSENZVEIG, Herch Moysés. Curso de física básica: Fluidos, Oscilações e Ondas, Calor (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.

Por Pâmella Raphaella Melo
Professora de Física