Pressão

Pressão é uma grandeza escalar definida como o módulo da força aplicada dividida por unidades de área. A unidade de pressão no sistema internacional de unidades (SI) é o Pa (pascal), que equivale à aplicação de uma força de 1 N sobre uma área de 1 m². A definição de pressão é comumente utilizada para descrever a influência sobre o comportamento de fluidos, como gases e líquidos.

Tópicos deste artigo

• 1 - Resumo sobre pressão
• 2 - O que é pressão?
• 3 - Exemplo
• 4 - Resolução
• 5 - Pressão hidrostática
• 6 - O que é pressão atmosférica?
• 7 - Pressão absoluta
• 8 - Fórmulas de pressão
• 9 - Unidades de pressão
• 10 - Pressão arterial
• 11 - Exercícios sobre pressão, força e área
• 12 - Resolução
• 13 - Exercícios sobre pressão hidrostática
• 14 - Resolução

Resumo sobre pressão

• Pressão é definida pela razão entre a força aplicada sobre o tamanho da superfície de contato.

• Pressão hidrostática é o nome dado à pressão produzida por um determinado fluido em equilíbrio estático (repouso).

• A unidade de pressão no sistema internacional de unidades (SI) é o pascal, que é equivalente à aplicação de uma força de 1 N em uma área de 1 m².

• Pressão absoluta é o nome dado à soma da pressão hidrostática com a pressão atmosférica.

O que é pressão?

Pressão é a expressão de uma força aplicada sobre uma área. Pode ser expressa a partir da equação abaixo:

Legenda:
P – pressão
F – força aplicada
A – área

De acordo com o sistema internacional de unidades (SI), a unidade de pressão é o pascal (Pa). A pressão de 1 Pa equivale à aplicação de uma força de 1 N sobre uma área de 1 m²:

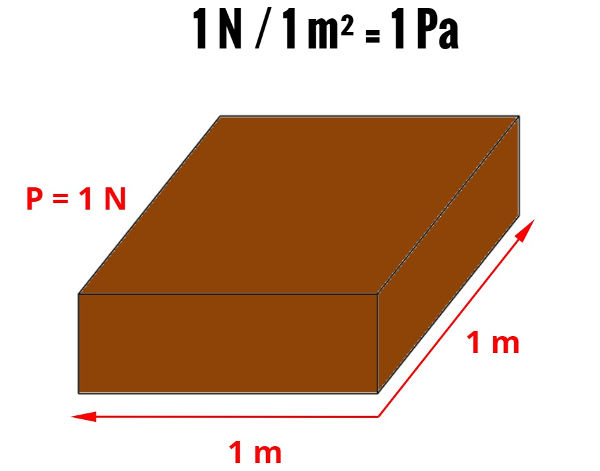
O bloco mostrado na figura acima tem peso de 1 N, e a área de sua superfície inferior é de 1 m². Logo, a pressão exercida por ele é de 1 Pa.

Pressão é uma variável importante em diversas situações, por exemplo: ao amolar uma faca, reduzimos sua área de contato, aumentando, assim, a pressão exercida, facilitando o corte. Quanto menor for a área de contato entre dois corpos, maior será a pressão exercida, independentemente se aumentarmos ou diminuirmos a força aplicada. Observe o exemplo abaixo:

Exemplo

a) Calcule a pressão exercida pelos pés de uma mulher de massa igual a 60,0 kg. Considere que a mulher encontra-se em pé e que a área total de seus pés seja de 120 cm².

Dados: g = 10 m/s².

b) Assuma agora que a mulher esteja usando sapatos de salto alto e que a área total desses saltos seja de, aproximadamente, 4 cm². Nesse caso, qual será o módulo da pressão exercida sobre o solo?

Resolução

a) Como sabemos, a pressão é dada pela razão entre a força aplicada e a área de contato. A força, no caso do exercício, é a força peso, definida pelo produto da massa da mulher (60,0 kg) pela gravidade local (10 m/s²). Além disso, a área de contato deve ser expressa no sistema internacional de unidades, ou seja, em m². Para tanto, basta dividirmos a área de 120 cm² pelo fator (10²)², resultando em 0,012 m². Dessa forma, teremos o seguinte cálculo:
 

b) No caso em que a mulher está usando saltos altos, podemos calcular a pressão exercida no solo para a nova área de 4 cm² (0,0004 m²):
 

Pelos resultados encontrados acima, é possível perceber que a pressão pode sofrer grandes variações de acordo com a área de contato entre os corpos. No caso do exemplo, a pressão variou enormemente, saindo de 50.000 Pa para 1.500.000 Pa.

Pressão hidrostática

Pressão hidrostática é a pressão exercida por fluidos em repouso. Para calcularmos essa pressão, utilizamos uma relação matemática um pouco diferente, porém mais útil para o estudo dos fluidos.

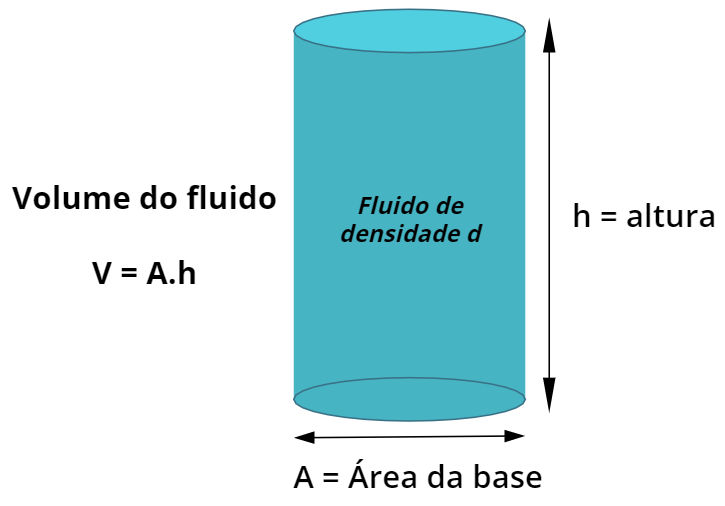
Imagine um cilindro de massa desprezível, completamente preenchido por um fluido qualquer, como mostra a figura abaixo:

Veja também: Fundamentos da Hidrostática

A pressão exercida por esse fluido pode ser calculada por meio da relação clássica de pressão (P = F/A). Entretanto, se levarmos em conta que a massa do fluido (m) relaciona-se com outras duas propriedades do fluido, seu volume (V) e sua densidade (d), poderemos deduzir a seguinte fórmula de pressão hidrostática:
 

A pressão hidrostática, também conhecida como pressão manométrica, é dada pela expressão matemática P = dgh.

Legenda:

d – densidade do fluido (kg/m³)

V – volume do fluido (m³)

A – área da base do recipiente (m²)

h – altura do fluido que ocupa o recipiente (m)

De acordo com o cálculo acima, a pressão exercida por um fluido em equilíbrio estático é dada pela expressão P = dgh, ou seja, quanto maior for a profundidade de um fluido, maior será a pressão exercida por ele.

O que é pressão atmosférica?

Pressão atmosférica é a pressão exercida pela coluna de gases atmosféricos presente acima de nós durante todo o tempo. A atmosfera terrestre é composta por gases leves, como nitrogênio, oxigênio, gás carbônico, por isso, apresenta uma densidade relativamente baixa. Ao nível do mar, sua densidade é de aproximadamente 1,2 kg/m³. À medida que nos encontramos mais altos em relação ao nível do mar, a densidade atmosférica tende a cair, e seus gases tornam-se cada vez mais rarefeitos até uma fronteira de centenas de quilômetros, quando se inicia o vácuo espacial.

Veja também: Para que serve um manômetro?

A pressão atmosférica ao nível do mar foi determinada pela primeira vez pelo físico italiano Evangelista Torricelli, ex-aluno do físico inventor do barômetro de mercúrio (instrumento utilizado para medidas de pressão), o também italiano Galileu Galilei. Para tanto, Torricelli utilizou um tubo cilíndrico de vidro de 1 m de altura preenchido com mercúrio. Ao verter o conteúdo do tubo em um recipiente cheio de mercúrio, Torricelli percebeu que a altura do líquido dentro do tubo de vidro permanecia estática em 76 cm (760 mm). Dessa forma, definiu que a pressão atmosférica era de módulo igual ao da pressão exercida por uma coluna de 760 milímetros de mercúrio:

P₀ = 760 mmHg = 1 atm

Legenda:
P₀ – pressão atmosférica
atm – pressão exercida pela atmosfera terrestre ao nível do mar
mmHg – pressão exercida por uma coluna de mercúrio

Veja também: Como Torricelli mediu a pressão atmosférica?

Pressão absoluta

Pressão absoluta é a pressão total exercida sobre um corpo na superfície da Terra. Para calcularmos a pressão absoluta sobre um corpo, devemos levar em conta a atuação de duas pressões distintas: a pressão atmosférica e a pressão manométrica (exercida por um fluido).

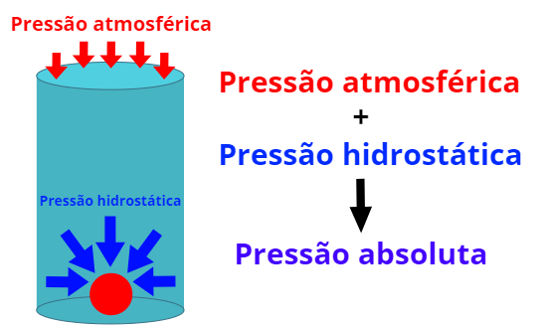
A pressão absoluta exercida sobre um corpo imerso em um fluido é a soma da pressão atmosférica com a pressão hidrostática.

A relação estabelecida entre a pressão atmosférica e a pressão hidrostática é chamada de Teorema de Stevin e é definida pela equação abaixo:

Legenda:
P – pressão absoluta
P₀ – pressão atmosférica
dgh – pressão manométrica ou hidrostática

Fórmulas de pressão

Confira algumas fórmulas utilizadas para o cálculo da pressão:

→ Utilize a fórmula abaixo para calcular a pressão exercida sobre uma área:

Legenda:
P – pressão
F – força aplicada
A – área

→ A fórmula a seguir pode ser usada para determinar a pressão exercida por um fluido em equilíbrio estático. Denominamos esse tipo de pressão como pressão hidrostática ou pressão manométrica:

Legenda:
P – pressão hidrostática (Pa)
d – densidade do fluido (kg/m³)
g – gravidade local (m/s²)
h – altura do fluido(m)

→ A fim de calcularmos a pressão absoluta sobre um corpo que esteja imerso em um fluido sob a ação da pressão atmosférica, podemos utilizar o Teorema de Stevin:

Legenda:
P – pressão absoluta
P₀ – pressão atmosférica
dgh – pressão manométrica ou hidrostática

Unidades de pressão

Existem muitas unidades utilizadas para medir a pressão em diferentes partes do mundo ou na realização de diferentes atividades. É importante conhecermos algumas delas e sabermos como convertê-las para a unidade padrão, o pascal:

Para simplificação dos cálculos, é comum encontrarmos livros didáticos que trazem a informação de que 1 atm equivale a 1,01.10⁵ Pa ou a 760 mmHg.

1 atm = 1,01.10⁵ Pa = 760 mmHg

Pressão arterial

Pressão arterial é a pressão exercida pelo sangue contra as paredes das artérias. Para medirmos a pressão arterial, utilizamos um aparelho chamado esfigmomanômetro. Esse aparelho é capaz de medir as pressões sistólica e diastólica, que são, respectivamente, as pressões do sangue ao sair e ao retornar ao coração.

O resultado exibido nos ponteiros ou nos displays do esfigmomanômetro informa a razão entre as pressões produzidas pela contração e pelo relaxamento cardíaco. De acordo com a Sociedade Brasileira de Cardiologia (SBC), a razão dessas pressões considerada saudável é a de 120 mmHg de pressão sistólica por 80 mmHg de pressão diastólica, comumente denotado como uma pressão de 12:8 (doze por oito).

O aumento crônico da pressão arterial é um fator de risco para o surgimento de doenças cardíacas e recebe o nome de hipertensão. A hipertensão pode surgir em decorrência de fatores como má alimentação, sedentarismo, excesso de peso e obesidade, consumo de bebidas alcoólicas e, até mesmo, fatores genéticos. Confira a tabela fornecida pela SBC para a determinação da hipertensão arterial:

Veja também: Diferença entre pressão alta e pressão baixa

Exercícios sobre pressão, força e área

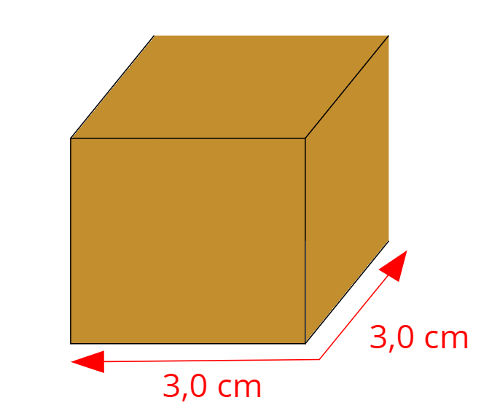
Um cubo maciço, assim como o da figura abaixo, de aresta 3,0 cm e massa igual a 10,0 g encontra-se apoiado sobre uma superfície lisa e horizontal. Sendo a aceleração da gravidade local g = 10 m/s², calcule a pressão que esse objeto exerce sobre a superfície.

Resolução

Começaremos dando atenção às unidades fornecidas pelo enunciado do exercício. Para tanto, devemos lembrar que todas elas devem ser expressas no sistema internacional de unidades (S.I.). Dessa forma, a aresta do cubo tem comprimento de 0,03 m (3 cm), e sua massa é de 0,010 kg (10,0 g).

Para calcularmos a pressão exercida pela face inferior do cubo, aquela sobre a qual se apoia, utilizaremos a definição mais simples de pressão:

Como já sabemos, a força exercida pelo cubo é a força normal de compressão, que, no caso de uma superfície horizontal, é numericamente igual ao seu peso. Portanto:
 

Exercícios sobre pressão hidrostática

Durante a execução de uma obra, um engenheiro deseja que a água saia de uma torneira com uma pressão máxima de 2,0 atm a fim de evitar possíveis danos ao sistema hidráulico. Para isso, qual deverá ser a mínima altura que as caixas d'águas devem ser instaladas a partir da altura dessa torneira?

Dados:

1 atm = 1,01.10⁵ Pa

g = 10 m/s²

d_água = 1000 kg/m³

Resolução

Para calcularmos a altura mínima que as caixas d'água devam ser instaladas, é necessário lembrar que existe ar atmosférico no interior delas. Por isso, não basta calcularmos somente a pressão hidrostática da água, devemos levar em conta sua pressão absoluta por meio do Teorema de Stevin:

Portanto, considerando a pressão absoluta igual a 2 atm (2 x 1,01.10⁵ Pa), teremos a seguinte resolução:

Por Me.Rafael Helerbrock