Segunda lei de Kepler

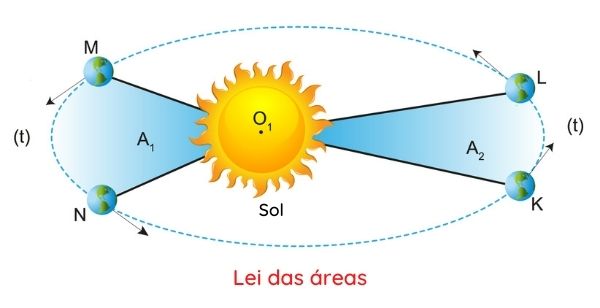
A segunda lei de Kepler, também conhecida como lei das áreas, foi criada por Johannes Kepler para explicar a exótica orbita de Marte que fora observada. Essa lei descreve que um corpo orbitando ao redor de outro, esse último em um referencial de repouso, percorrerá áreas iguais em intervalos de tempo iguais.

A principal consequência dessa lei é a variação que ocorre na velocidade orbital, pois, quando o planeta estiver no periélio, ou seja, mais perto do Sol, terá velocidade maior, mas, se estiver no afélio, ou seja, mais distante do Sol, terá velocidade menor.

Leia também: Três erros comuns cometidos no estudo da gravitação universal

Tópicos deste artigo

• 1 - Resumo sobre a segunda lei de Kepler
• 2 - O que diz a segunda lei de Kepler?
• 3 - Fórmula da segunda lei de Kepler
• 4 - Como aplicar a segunda lei de Kepler?
• 5 - Videoaula sobre as leis de Kepler
• 6 - Exercícios resolvidos sobre a segunda lei de Kepler

Resumo sobre a segunda lei de Kepler

• Johannes Kepler foi o físico responsável pelo estudo e pelas observações contidas nas três leis de Kepler.

• As leis de Kepler foram desenvolvidas com base nas constatações de Johannes Kepler sobre a órbita de Marte.

• As órbitas ao redor do Sol descrevem trajetórias elípticas, em que o Sol está em um dos focos da elipse.

• A segunda lei de Kepler descreve que corpos orbitando ao redor de outro corpo em repouso fazem deslocamentos de áreas iguais em intervalos de tempos iguais.

• Essa lei é consequência do princípio de conservação do momento angular.

• A velocidade orbital do planeta no periélio é maior que no afélio.

O que diz a segunda lei de Kepler?

Baseado nas observações e comprovações a respeito da orbita excêntrica de Marte, que descrevia um movimento elíptico e com velocidades orbitais variando de acordo com sua aproximação e afastamento do Sol, Johannes Kepler (1571-1630) desenvolveu sua segunda lei, também chamada de lei das áreas.

O enunciado da segunda lei de Kepler diz o seguinte:

“O raio vetor que liga um planeta ao Sol descreve áreas iguais em tempos iguais.”

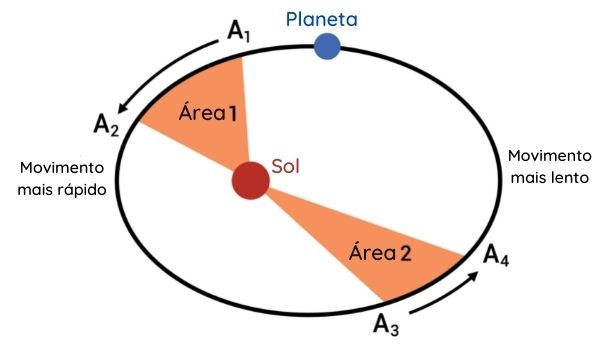
Usando a figura como exemplo, a lei nos descreve que o tempo para percorrer a área 1 será o mesmo para a área 2, desde que essas áreas sejam iguais, ainda que aparentem ser de tamanhos diferentes.

Em consequência disso, a velocidade orbital sofre alterações, em que, se o corpo estiver mais perto do Sol (periélio), a velocidade será maior, mas, se estiver mais distante (afélio), ela será menor.

V_Periélio > V_Afélio

Vale ressaltar que as leis de Kepler não funcionam apenas para as órbitas dos planetas ao redor do Sol, mas também para qualquer corpo orbitando ao redor de outro que está em repouso e quando a interação entre eles é gravitacional.

Como exemplo temos os satélites naturais, como a Lua, que orbita ao redor da Terra, e as luas de Saturno, que orbitam ao redor desse planeta, seguindo essas leis. Nesses casos, a Terra e Saturno são os referencias em repouso respectivamente.

Leia também: O que aconteceria se a Terra parasse de girar?

Fórmula da segunda lei de Kepler

A fórmula que descreve a segunda lei de Kepler é:

\(\frac {A_1}{∆t_1}=\frac{A_2}{∆t_2}\)

• \(A_1\ \)e \(A_2\)são as áreas compreendidas pelo movimento, medidas em .

• \(∆t_1\)e \(∆t_2 \)são as variações do tempo ocorridas no deslocamento, medidas em segundos.

Como aplicar a segunda lei de Kepler?

Utiliza-se a segunda lei de Kepler sempre que se trabalha com deslocamentos de corpos celestes com áreas iguais e, consequentemente, em intervalos de tempos iguais.

Assim, pode-se utilizá-la no estudo do movimento dos planetas ao redor do Sol ou de outras estrelas; dos satélites naturais e artificiais ao redor dos planetas, entre outros.

Videoaula sobre as leis de Kepler

Exercícios resolvidos sobre a segunda lei de Kepler

Questão 01

(Unesp) Analise o movimento de um planeta em diversos pontos de sua trajetória em torno do Sol, conforme aparece na figura A. Considerando os trechos entre os pontos A e B e entre os pontos C e D, pode-se afirmar que,

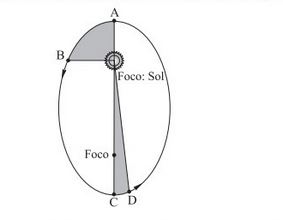
(A) entre A e B, a área varrida pela linha que liga o planeta ao Sol é maior do que aquela entre C e D.

(B) caso as áreas sombreadas sejam iguais, o planeta move-se com maior velocidade escalar no trecho entre A e B.

(C) caso as áreas sombreadas sejam iguais, o planeta move-se com maior velocidade escalar no trecho entre C e D.

(D) caso as áreas sombreadas sejam iguais, o planeta move-se com a mesma velocidade nos dois trechos.

(E) caso as áreas sombreadas sejam iguais, o tempo levado para o planeta ir de A até B é maior que entre C e D.

Resolução:

Alternativa B. Considerando que as áreas sombreadas sejam iguais, pela segunda lei de Kepler, pode-se deduzir que o planeta se moverá com uma velocidade maior no periélio, quando estiver mais perto do Sol, e com menor velocidade no afélio, quando estiver mais longe do Sol. Então, no intervalo AB, ele terá maior velocidade escalar.

Questão 2

(Unesp) A órbita de um planeta é elíptica e o Sol ocupa um de seus focos, como ilustrado na figura (fora de escala). As regiões limitadas pelos contornos OPS e MNS têm áreas iguais a A.

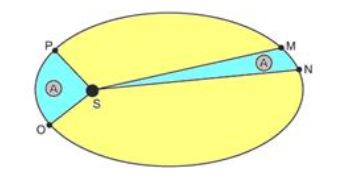
Se \(t_OP\) e \(t_MN\) são os intervalos de tempo gastos para o planeta percorrer os trechos OP e MN, respectivamente, com velocidades médias \(v_OP\) e \( v_MN\), pode-se afirmar que:

a) \(t_OP>t_MN \) e \(v_OP

b) \( t_OP=t_MN \) e \(v_OP>v_MN\)

c) \( t_OP=t_MN \) e \(v_OP

d) \( t_OP>t_MN\) e \(v_OP>v_MN\)

e) \( t_OP e \(v_OP

Resolução:

Alternativa B. Segundo a segunda lei de Kepler, as regiões limitadas pelos contornos OPS e MNS ocorrem em intervalos de tempos iguais, portanto \(t_OP=t_MN\). Além disso, a velocidade no períelio será maior que no afélio, então \(v_OP>v_MN\).

Por Pâmella Raphaella Melo
Professora de Física