Terceira lei de Kepler

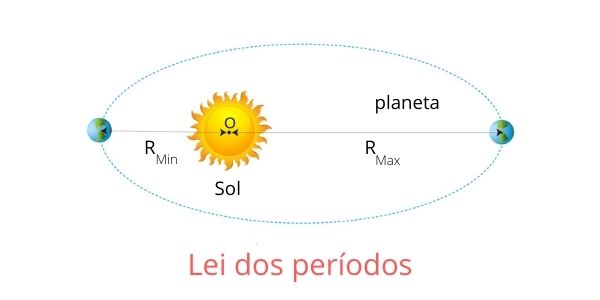
A terceira lei de Kepler, também conhecida como lei dos períodos, foi criada por Johannes Kepler baseada nos dados obtidos em seus estudos e nas observações de Tycho Brahe.

Essa lei relaciona a distância do Sol com o tempo do movimento de translação, em que o cubo do raio médio da órbita do planeta é diretamente proporcional ao quadrado do período de translação do planeta ao redor do Sol. Assim, quanto maior for o tempo de translação, maior será nossa distância em relação ao astro.

Leia também: 1ª lei de Kepler — aquela que enuncia a trajetória elíptica dos planetas em torno do Sol

Tópicos deste artigo

• 1 - Resumo sobre a terceira lei de Kepler
• 2 - O que afirma a terceira lei de Kepler?
• 3 - Fórmula da terceira lei de Kepler
• 4 - Como aplicar a terceira lei de Kepler?
• 5 - Videoaula sobre as leis de Kepler
• 6 - Exercícios resolvidos sobre a terceira lei de Kepler

Resumo sobre a terceira lei de Kepler

• Johannes Kepler foi o físico responsável pelo estudo e observações a respeito das três leis de Kepler.
• As leis de Kepler foram desenvolvidas a partir das suas constatações sobre a órbita de Marte e baseadas nos estudos de Tycho Brahe.
• As órbitas ao redor do Sol descrevem trajetórias elípticas, sendo que o Sol está em um dos focos da elipse.
• A terceira lei de Kepler descreve que o quadrado do período de revolução do planeta é proporcional ao cubo do raio médio da órbita.
• O cubo do raio médio da órbita do planeta é diretamente proporcional ao quadrado do período de translação.

O que afirma a terceira lei de Kepler?

Desde sua juventude, Johannes Kepler (1571–1630) era obstinado em encontrar um padrão que relacionasse os raios médios das órbitas dos planetas com seus períodos de revolução (ou de translação). Apenas muitos anos após a formulação das suas duas primeiras leis, baseado nos dados obtidos trabalhando 17 anos nas observações de Tycho Brahe (1546–1601) e após muitas tentativas ineficazes, em 1618 Kepler formulou sua terceira lei. Entretanto, ele apenas a publicou em 1619, no prefácio de seu livro Harmonices mundi.

A terceira lei de Kepler diz o seguinte:

“Os quadrados dos períodos de revolução de dois planetas quaisquer estão entre si como os cubos de suas distâncias médias ao Sol.”

Essa lei aponta a relação existente entre a distância do planeta ao Sol e seu período de revolução (ou translação). Quanto mais distante um planeta estiver do Sol, mais tempo aquele levará para completar sua volta em torno deste.

Vale ressaltar que como existe a interação gravitacional entre os corpos no espaço, há um pequeno erro nos cálculos utilizando as leis de Kepler. Mas como no caso do sistema Sol-planetas o centro de massa está praticamente no Sol, podemos aplicá-las com grande precisão, até mesmo em massas menores, como no sistema Terra-Lua ou satélites mais distantes. Há uma aproximação significativa entre a dinâmica real dos movimentos dos corpos e a teoria.

Ainda que seja comumente usada com corpos do Sistema Solar, assim como as outras duas leis, a terceira lei de Kepler também é válida para quaisquer corpos celestes, desde que o corpo central esteja em um referencial em repouso, ou seja, fixo.

Fórmula da terceira lei de Kepler

Baseada nesse contexto, a fórmula que descreve a segunda lei é:

\(\frac{T^2}{R^3}=constante\)

• T  é o período de revolução do planeta, medido em horas ou anos.
• R é o raio médio da órbita do planeta, medido em quilômetros ou UA.

O cubo do raio médio da órbita do planeta (ou seja, \(R^3\)) é diretamente proporcional ao quadrado do período de translação (ou seja, \(T^2\)) do corpo celeste ao redor do Sol.

Entretanto, para calcular o que desejamos, comparamos dois planetas ou dois corpos celestes, utilizando a fórmula:

\(\frac{{T_1}^2}{{R_1}^3}=\frac{{T_2}^2}{{R_2}^3}\)

• \(T_1\)e \(T_2\) são os períodos de revolução de dois planetas.
• \(R_1\) e \(R_2\) são os raios médios das órbitas desses dois planetas.

Na maioria dos exercícios são apresentados os valores do raio e do período. Porém, caso não sejam oferecidos, você pode consultar a tabela abaixo com os valores referentes aos planetas do Sistema Solar.|1|

Observação: UA é a unidade astronômica. Ela equivale à distância da Terra ao Sol (1,48 x 10⁸ km). Esses valores estão, portanto, relacionados com a Terra. Mercúrio, por exemplo, leva 0,241 anos terrestres para dar uma volta ao redor do Sol.

Leia também: Lei de Hubble e a expansão do Universo

Como aplicar a terceira lei de Kepler?

Em questões sobre o assunto, utilizaremos a terceira lei de Kepler sempre que os exercícios envolverem períodos de translação e raios de órbitas.

Já em relação à pesquisa de forma geral, podemos utilizá-la nos estudos da Astronomia e Astrofísica. Ela é empregada quando é necessário descobrir períodos de revolução ou distâncias em relação com algum planeta, estrela ou outros corpos celestes.

Videoaula sobre as leis de Kepler

Exercícios resolvidos sobre a terceira lei de Kepler

Questão 1

(Unicamp — adaptada) A terceira lei de Kepler diz que “o quadrado do período de revolução de um planeta (tempo gasto para dar uma volta em torno do Sol) dividido pelo cubo da distância média do planeta ao Sol é uma constante”. A distância média da Terra ao Sol é equivalente a 1 UA (unidade astronômica).

Entre Marte e Júpiter, existe um cinturão de asteroides (vide figura).

Os asteroides são corpos sólidos que teriam sido originados do resíduo de matérias existentes por ocasião da formação do Sistema Solar.

Se no lugar do cinturão de asteroides essa matéria tivesse se aglutinado formando um planeta, quanto duraria o ano desse planeta em anos terrestres se sua distância em relação ao Sol fosse de 2,5 UA?

Resolução

Utilizando a terceira lei de Kepler, assumindo que o lado esquerdo da fórmula é referente ao planeta Terra e o lado direito da fórmula é referente ao planeta em questão, temos:

\(\frac{{T_1}^2}{{R_1}^3}=\frac{{T_2}^2}{{R_2}^3}\)

\(\frac{1^2}{1^3}=\frac{{T_2}^2}{{2,5}^3}\)

\(\frac{1}{1}=\frac{{T_2}^2}{15,625}\)

\(15,625={T_2}^2\)

\(\sqrt{15,625}={T_2}^2\)

\(3,95\cong{T_2}^2\)

O período duraria aproximadamente 3,95 anos terrestres.

Questão 2

(Vunesp) Grande parte dos satélites de comunicação estão localizados em órbitas circulares que estão no mesmo plano do equador terrestre. Geralmente, esses satélites são geoestacionários, isto é, possuem período orbital igual ao período de rotação da Terra, 24 horas.

Considerando que a órbita de um satélite geoestacionário possui raio orbital de 42.000 km, um satélite em órbita circular no plano do Equador, com raio orbital de 10.500 km, tem período orbital de:

a) 3 horas

b) 4 horas

c) 5 horas

d) 6 horas

e) 8 horas

Resolução

Alternativa A

Utilizando a fórmula da terceira lei de Kepler e substituindo as variáveis pelos valores dados no enunciado:

\(\frac{{T_1}^2}{{R_1}^3}=\frac{{T_2}^2}{{R_2}^3}\)

\(\frac{{24}^2}{{42000}^3}=\frac{{T_2}^2}{{10500}^3}\)

\(\frac{576}{7,4088.{10}^{13}}=\frac{{T_2}^2}{{1,157625.10}^{12}}\)

\(\frac{576.{1,157625.10}^{12}}{7,4088.{10}^{13}}={T_2}^2\)

\(90.{10}^{12-13}={T_2}^2\)

\(9.{10}^1.{10}^{-1}={T_2}^2\)

\(9={T_2}^2\)

\(\sqrt9=T_2\)

\(3=T_2\)

Notas

|1| Dados da tabela foram retirados de: NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.

Por Pâmella Raphaella Melo
Professora de Física