Leis de Kepler

Leis de Kepler sobre o movimento planetário foram desenvolvidas entre 1609 e 1619 pelo astrônomo e matemático alemão Johannes Kepler. As três leis de Kepler, usadas para descrever as órbitas dos planetas do Sistema Solar, foram construídas com base em medidas astronômicas precisas, obtidas pelo astrônomo dinamarquês Tycho Brahe.

Veja também: História da astronomia

Tópicos deste artigo

• 1 - Introdução às leis de Kepler
• 2 - Leis de Kepler
• 3 - 1ª lei de Kepler: lei das órbitas
• 4 - 2ª lei de Kepler: lei das áreas
• 5 - 3ª lei de Kepler: lei dos períodos ou lei da harmonia
• 6 - Exercícios sobre leis de Kepler

Introdução às leis de Kepler

As contribuições deixadas por Nicolau Copérnico na área da astronomia romperam com a visão geocentrista do Universo, derivada do modelo planetário de Claudio Ptolomeu. O modelo sugerido por Copérnico, embora complexo, permitiu a previsão e a explicação das órbitas de diversos planetas, entretanto, apresentava algumas falhas, sendo a mais dramática delas uma explicação satisfatória para a órbita retrógrada de Marte durante alguns períodos do ano.

A resolução dos problemas inexplicáveis pelo modelo planetário de Copérnico veio somente no século XVII, pelas mãos de Johannes Kepler. Para tanto, Kepler admitiu que as órbitas planetárias não eram perfeitamente circulares, mas sim elípticas. Em posse de dados astronômicos extremamente precisos, realizados por Brahe, Kepler estabeleceu duas leis que regem o movimento dos planetas, 10 anos depois, publicou uma terceira lei, que permite estimar o período orbital ou até mesmo o raio da órbita dos planetas que giram em torno do Sol.

Leis de Kepler

As leis do movimento planetário de Kepler são conhecidas como: lei das órbitas elípticas, lei das áreas e lei dos períodos. Juntas estas explicam como funciona o movimento de qualquer corpo orbitando algum astro massivo, como planetas ou estrelas. Vamos conferir o que se afirma nas leis de Kepler:

1ª lei de Kepler: lei das órbitas

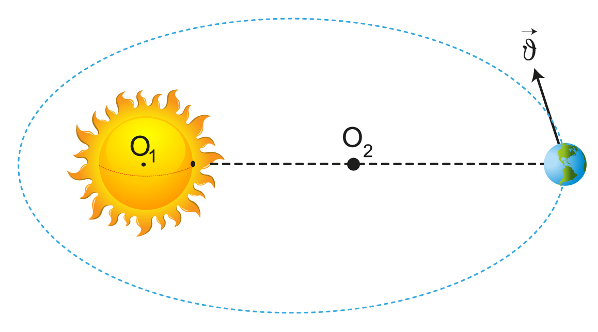
A primeira lei de Kepler afirma que a órbita dos planetas que giram em torno do Sol não é circular, mas sim elíptica. Além disso, o Sol sempre ocupa um dos focos dessa elipse. Apesar de elípticas, algumas órbitas, como a da Terra, são muito próximas de um circulo, pois são elipses que apresentam uma excentricidade muito pequena. A excentricidade, por sua vez, é a medida que mostra o quanto uma figura geométrica difere-se de um círculo e pode ser calculada pela relação entre os semieixos da elipse.

“A órbita dos planetas é uma elipse em que o Sol ocupa um dos focos.”

2ª lei de Kepler: lei das áreas

A segunda lei de Kepler afirma que a linha imaginária que liga o Sol aos planetas que o orbitam varre áreas em intervalos de tempo iguais. Em outras palavras, essa lei afirma que a velocidade com que as áreas são varridas é igual, isto é, a velocidade aureolar das órbitas é constante.

“A linha imaginária que liga o Sol aos planetas que o orbitam varre áreas iguais em intervalos de tempos iguais.”

3ª lei de Kepler: lei dos períodos ou lei da harmonia

A terceira lei de Kepler afirma que o quadrado do período orbital (T²) de um planeta é diretamente proporcional ao cubo de sua distância média ao Sol (R³). Além disso, a razão entre T² e R³ tem exatamente a mesma magnitude para todos os astros que orbitam essa estrela.

“A razão entre o quadrado do período e o cubo do raio médio da órbita de um planeta é constante.”

A expressão usada para o cálculo da terceira lei de Kepler é mostrada a seguir, confira:

T – período orbital

R – raio médio da órbita

Observe a próxima figura, nela mostramos os semieixos maior e menor de uma órbita planetária em torno do Sol:

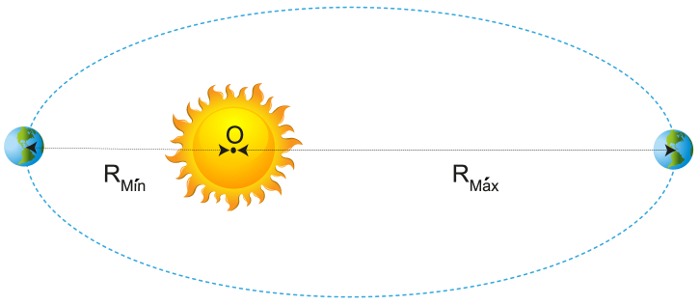
O raio médio da órbita, utilizado no cálculo da terceira lei de Kepler, é dado pela média entre os raios máximo e mínimo. As posições mostradas na figura, que caracterizam a maior e a menor distância da Terra em relação ao Sol, são chamadas de afélio e periélio, respectivamente.

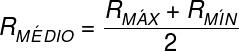
Quando a Terra aproxima-se do periélio, sua velocidade orbital aumenta, uma vez que a aceleração gravitacional do Sol intensifica-se. Dessa maneira, a Terra tem máxima energia cinética quando nas proximidades do periélio. Aproximando-se do afélio, ela perde energia cinética, tendo assim a sua velocidade orbital reduzida à sua menor medida.

A fórmula mais detalhada da terceira lei de Kepler é mostrada a seguir. Observe que a razão entre T² e R³ é determinada exclusivamente por duas constantes, o número pi e a constante da gravitação universal, e também pela massa do Sol:

G – constante da gravitação universal (6,67.10^-11 N.m²/kg²)

M – massa do Sol (1,989.10³⁰ kg)

Essa lei não foi obtida por Kepler, mas sim por Isaac Newton, por meio da lei da gravitação universal. Para fazê-lo, Newton identificou que a força de atração gravitacional entre a Terra e o Sol é uma força centrípeta. Observe o cálculo seguinte, nele se mostra como é possível obter, com base na lei da gravitação universal, a expressão geral da terceira lei de Kepler:

Confira a tabela seguinte, nela mostramos como variam as medidas de T² e R³, além de sua razão, para cada um dos planetas do Sistema Solar:

O raio médio das órbitas, na tabela, é medido em unidades astronômicas (ua). Uma unidade astronômica corresponde à distância média entre a Terra e o Sol, cerca de 1,496.10¹¹ m. Além disso, as pequenas variações nas razões T² sobre R³ devem-se às limitações de precisão nas medidas do raio orbital e do período de translação de cada planeta.

Leia também: O que aconteceria se a Terra parasse de girar?

Exercícios sobre leis de Kepler

Questão 1

(ITA 2019) Uma estação espacial, Kepler, estuda um exoplaneta cujo satélite natural tem órbita elíptica de semieixo maior a₀ e período T₀, sendo d = 32a₀ a distância entre a estação e o exoplaneta. Um objeto que se desprende de Kepler é atraído gravitacionalmente pelo exoplaneta e inicia um movimento de queda livre a partir do repouso em relação a esse. Desprezando a rotação do exoplaneta, a interação gravitacional entre o satélite e o objeto, bem como as dimensões de todos os corpos envolvidos, calcule em função de T₀ o tempo de queda do objeto.

Gabarito: t = 32T₀

Resolução:

Se levarmos em conta que a excentricidade da trajetória elíptica que o objeto descreverá é aproximadamente igual a 1, podemos assumir que o raio da órbita do objeto será igual à metade da distância entre a estação espacial Kepler e o planeta. Desse modo, calcularemos qual deve ser o tempo em que o objeto aproxima-se do planeta, a partir de sua posição inicial. Para tanto, devemos encontrar o período da órbita, e o tempo de queda, por sua vez, será igual à metade desse tempo:

Depois de termos aplicado a terceira lei de Kepler, dividimos o resultado por 2, uma vez que o que calculamos foi o período orbital, em que, na metade do tempo, o objeto cai em direção ao planeta, e na outra metade, afasta-se. Desse modo, o tempo de queda, em termos de T₀, é igual a 32T₀.

Questão 2

(Udesc 2018) Analise as proposições com relação às leis de Kepler sobre o movimento planetário.

I. A velocidade de um planeta é maior no periélio.

II. Os planetas movem-se em órbitas circulares, estando o Sol no centro da órbita.

III. O período orbital de um planeta aumenta com o raio médio de sua órbita.

IV. Os planetas movem-se em órbitas elípticas, estando o Sol em um dos focos.

V. A velocidade de um planeta é maior no afélio.

Assinale a alternativa correta.

a) Somente as afirmativas I, II e III são verdadeiras.

b) Somente as afirmativas II, III e V são verdadeiras.

c) Somente as afirmativas I, III e IV são verdadeiras.

d) Somente as afirmativas III, IV e V são verdadeiras.

e) Somente as afirmativas I, III e V são verdadeiras.

Gabarito: Letra C

Resolução:

Vamos analisar as alternativas:

I – VERDADEIRO. Quando o planeta aproxima-se do periélio, sua velocidade translacional aumenta, em razão do ganho de energia cinética.

II – FALSO. As órbitas planetárias são elípticas, com o Sol ocupando um de seus focos.

III – VERDADEIRO. O período orbital é proporcional ao raio da órbita.

IV – VERDADEIRO. Essa afirmação é confirmada pelo enunciado da primeira lei de Kepler.

V – FALSO. A velocidade de um planeta é maior nas proximidades do periélio.

Questão 3

(UFJF) Muitas teorias sobre o Sistema Solar sucederam-se, até que, no século XVI, o polonês Nicolau Copérnico apresentou uma versão revolucionária. Para Copérnico, o Sol, e não a Terra, era o centro do Sistema. Atualmente, o modelo aceito para o Sistema Solar é, basicamente, o de Copérnico, feitas as correções propostas pelo alemão Johannes Kepler e por cientistas subsequentes.

Sobre gravitação e as leis de Kepler, considere as afirmativas, a seguir, verdadeiras (V) ou falsas (F).

I. Adotando-se o Sol como referencial, todos os planetas movem-se descrevendo órbitas elípticas, tendo o Sol como um dos focos da elipse.

II. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas iguais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.

III. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas proporcionais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.

IV. Para qualquer planeta do Sistema Solar, o quociente do cubo do raio médio da órbita pelo quadrado do período de revolução em torno do Sol é constante.

Assinale a alternativa CORRETA.

a) Todas as afirmativas são verdadeiras.

b) Apenas as afirmativas I, II e III são verdadeiras.

c) Apenas as afirmativas I, II e IV são verdadeiras.

d) Apenas as afirmativas II, III e IV são verdadeiras.

e) Apenas as afirmativas I e II são verdadeiras.

Gabarito: Letra C

Resolução:

I. VERDADEIRA. A afirmação é o próprio enunciado da primeira lei de Kepler.

II. VERDADEIRA. A afirmação coincide com a definição da segunda lei de Kepler.

III. FALSA. A determinação da segunda lei de Kepler, que decorre do princípio da conservação do momento angular, implica que as áreas varridas são iguais para intervalos de tempos iguais.

IV. VERDADEIRA. A afirmativa reproduz o enunciado da terceira lei de Kepler, também conhecida como lei dos períodos.

Por Me. Rafael Helerbrock