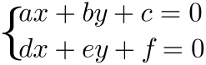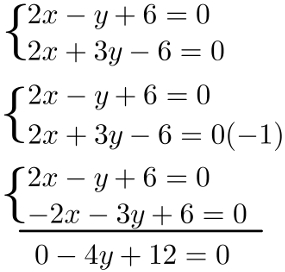Ponto de interseção entre duas retas

Uma reta é um conjunto de pontos que não faz curva. Em uma reta, existem infinitos pontos, o que também indica que a reta é infinita. A reta também pode ser considerada como espaço que possui apenas uma dimensão, ou seja, é na reta que se constroem figuras com uma dimensão ou menos.

Duas retas podem encontrar-se em 0, 1 ou 2 pontos. No primeiro caso, elas são chamadas paralelas; no segundo, elas são chamadas concorrentes e o ponto de encontro entre elas é chamado ponto de interseção; no terceiro caso, se duas retas possuem dois pontos em comum, então elas obrigatoriamente apresentam todos os pontos em comum e são chamadas coincidentes.

No caso em que duas retas têm um ponto de interseção (ou intersecção), sempre será possível encontrar as coordenadas desse ponto quando as equações dessas retas são conhecidas.

Coordenadas do ponto de interseção

Suponha que as retas ax + by + c = 0 e dx + ey + f = 0 encontram-se no ponto P(x_o, y_o). Note que os valores das incógnitas nesse ponto serão iguais para ambas as equações e que essa é justamente a definição de um sistema de equações com duas incógnitas e duas equações. Esse sistema pode ser escrito da seguinte maneira:

Assim, resolvendo esse sistema, encontraremos os valores de x e y que o tornam verdadeiro e que, ao mesmo tempo, são as coordenadas do ponto de encontro entre as duas retas que o formam.

Exemplo: Determine o ponto de encontro entre as retas 2x – y + 6 = 0 e 2x + 3y – 6 = 0

As coordenadas do ponto de interseção entre essas duas retas são dadas resolvendo o sistema formado:

Escolhemos o método da adição para resolver esse sistema, e isso não foi feito por nenhum motivo em especial. Prosseguindo na solução, basta resolver a equação encontrada:

– 4y + 12 = 0

– 4y = – 12 (– 1)

4y = 12

y = 12
      4

y = 3

Para finalizar, podemos substituir o valor de y em qualquer uma das equações:

2x – y + 6 = 0

2x – 3 + 6 = 0

2x + 3 = 0

2x = – 3

x = – 3  
       2 

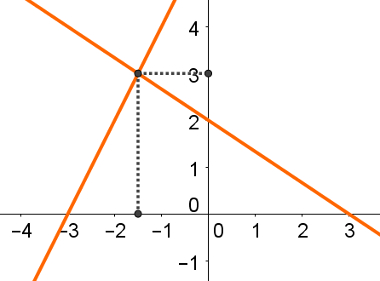
Assim, as coordenadas da interseção entre essas duas retas são: (3, – 3/2).

Observe as duas retas e seu ponto de encontro no seguinte gráfico:
 

Solução simplificada

A solução anterior é dada quando as equações estão em sua forma geral. Se as equações forem dadas em sua forma reduzida, a solução pode ser feita por outro método, com cálculos mais fácies e mais rápidos. Também podemos escrever as equações em sua forma reduzida antes de fazer os cálculos para evitar a solução do sistema.

A solução simplificada consiste em isolar uma das incógnitas das equações e igualar os seus resultados. Por exemplo, determine as coordenadas das retas de equações: x + y – 2 = 0 e 3x – y + 4 = 0.

Isolando uma incógnita de cada uma delas:

y = 2 – x e

y = 4 + 3x

Note que ambas as expressões em função de x são iguais a y. Como ambas são iguais ao mesmo número, então as expressões são iguais entre si:

2 – x = 4 + 3x

– x – 3x = 4 – 2

– 4x = 2

x = – 2
        4

x = – 1
        2
 

Substituindo o valor de x em uma das equações, encontraremos o valor de y:

y = 2 – x

y = 2 – 1
           2

y = 4 – 1
       2

y = 3
      2

Por Luiz Paulo Moreira
Graduado em Matemática

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

SILVA, Luiz Paulo Moreira. "Ponto de interseção entre duas retas"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/ponto-intersecao-entre-duas-retas.htm. Acesso em 11 de abril de 2021.