Média geométrica

A média geométrica junto à média aritmética e à média harmônica foram desenvolvidas pela escola pitagórica. Na estatística é bastante comum a busca pela representação de um conjunto de dados por um único valor para tomada de decisões. Uma das possibilidades para o valor central é a média geométrica.

Ela é útil para representação de um conjunto que possui dados que se comportam próximo a uma progressão geométrica, também para encontrar o lado de quadrado e cubo, conhecendo a área e o volume respectivamente. A média geométrica é aplicada também em situações de acumulação de aumento ou decrescimento percentual. Para calcular a média geométrica de um conjunto de n valores, calculamos a raiz enésima do produto dos elementos, ou seja, se um conjunto possui três termos, por exemplo, multiplicamos os três e calculamos a raiz cúbica do produto.

Tópicos deste artigo

• 1 - Fórmula da média geométrica
• 2 - Cálculo da média geométrica
• 3 - Aplicações da média geométrica
• 4 - Diferença entre média geométrica e média aritmética
• 5 - Exercícios resolvidos

Fórmula da média geométrica

A média geométrica é utilizada para encontrar um valor médio entre um conjunto de dados. Para calcular-se a média geométrica, é necessário um conjunto com dois ou mais elementos. Seja A um conjunto de dados A = (x₁, x₂, x₃, ... x_n), um conjunto com n elementos, a média geométrica desse conjunto é calculada por:

Leia também: Medidas de dispersão: amplitude e desvio

Cálculo da média geométrica

Seja A = {3,12,16,36}, qual será a média geométrica desse conjunto?

Resolução:

Para calcularmos a média geométrica, primeiro contamos a quantidade de termos do conjunto, no caso n = 4. Então temos que:

• Método 1: Realizando as multiplicações.

Como nem sempre temos à disposição a calculadora para realização das multiplicações, é possível fazer o cálculo com base na fatoração de um número natural.

• Método 2: Fatoração.

Utilizando as fatorações temos que:

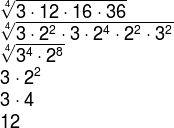
Aplicações da média geométrica

A média geométrica pode ser aplicada em qualquer conjunto de dados estatístico, mas normalmente ela é empregada na geometria, para comparar lados de prismas e cubos de mesmo volume, ou quadrados e retângulos de mesma área. Há também aplicação em problemas da matemática financeira que envolvam taxa percentual acumulada, ou seja, porcentagem sob porcentagem. Além de ser a média mais conveniente para dados que se comportam como uma progressão geométrica.

Exemplo 1: Aplicação em porcentagem.

Um produto, durante três meses, teve aumentos consecutivos, o primeiro foi de 20%, o segundo de 10% e o terceiro de 25%. Qual foi o aumento médio percentual ao final desse período?

Resolução

O produto custava inicialmente 100%, logo no primeiro mês ele passou a custar 120%, que, na sua forma decimal, escreve-se 1,2. Esse raciocínio será o mesmo para os três aumentos, então queremos a média geométrica entre: 1,2; 1,1; e 1,25.

O aumento é de 18,2% por mês em média.

Veja também: Cálculo de porcentagem com regra de três

Exemplo 2: Aplicação na geometria.

Qual deve ser o valor de x na imagem, sabendo que o quadrado e o retângulo, a seguir, possuem a mesma área?

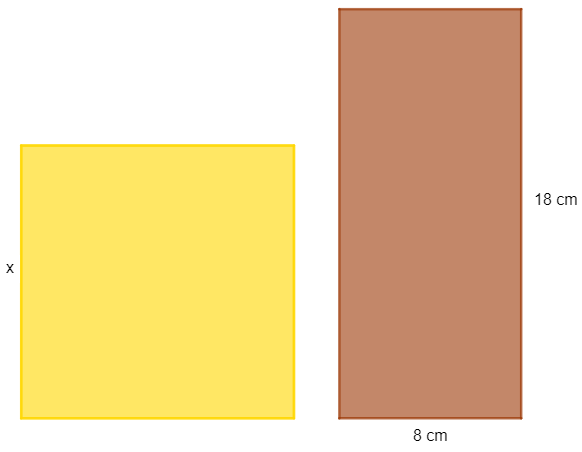
Resolução:

Para encontrarmos o valor x do lado do quadrado, calcularemos a média geométrica entre os lados do retângulo.

Logo, o lado do quadrado é 12 cm.

Exemplo 3: Progressão geométrica.

Quais são os termos da P.G., sabendo-se que o antecessor do valor central é x, o valor central é 10 e o sucessor do valor central é 4x.

Resolução:

Conhecemos os termos da P.G. (x,10,4x) e sabemos que a média geométrica entre o sucessor e o antecessor é igual ao termo central da P.G., então temos que:

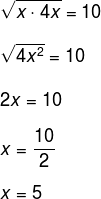
Diferença entre média geométrica e média aritmética

Na estatística, a forma como os dados comportam-se é muito importante para a escolha de um único valor para representá-los. Por isso existem tipos de medidas centrais e existem tipos de média.

A escolha sobre qual média utilizar deve ser feita levando-se em consideração o conjunto de dados que estamos trabalhando. Como visto no exemplo, se forem dados que se comportam próximo a uma progressão geométrica e que tenham o crescimento mais exponencial, recomenda-se a média geométrica.

Nas demais situações, em sua maioria utilizamos a média aritmética, por exemplo, o peso médio de um indivíduo ao decorrer do ano. Quando comparamos o cálculo dos dois tipos de média para um mesmo conjunto de dados, a geométrica sempre será menor que a aritmética.

Quando comparamos a fórmula da média aritmética com a da média geométrica, notamos a diferença, pois a primeira é calculada pela soma dos termos dividida pela quantidade de termos, já a segunda, como vimos, é calculada pela raiz enésima do produto de todos os termos.

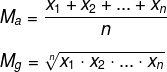
Exemplo 4: Dado o conjunto (3, 9, 27, 81, 243), perceba que ele é uma P.G. de razão 3, pois do primeiro para o segundo termo multiplicamos por três, do segundo para o terceiro também, e assim sucessivamente. Ao procurarmos um valor central para representar esse conjunto, o ideal é que ele seja o termo central da progressão, o que acontece se calcularmos a média geométrica. No entanto, quando se calcula a média aritmética, os valores maiores fazem com que o valor dessa média fique muito alto em relação aos termos do conjunto, e, quanto maior for o valor, mais distante de uma representação do termo central a média aritmética ficará.

Resolução:

1º Média aritmética

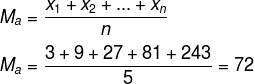
2º Média geométrica

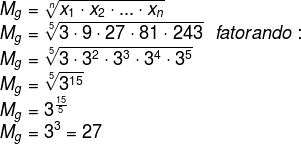
Acesse também: Moda, média e mediana – medidas de centralidade

Exercícios resolvidos

Questão 1 - O preço da gasolina no Brasil passou por grandes aumentos nos últimos meses. Os aumentos mensais dos últimos 4 meses foram, respectivamente, de 9%, 15%, 25% e 16%. Qual foi o aumento médio percentual nesse período?

a) 15%

b) 15,5%

c) 16%

d)14%

e) 14,5%

Resolução

Alternativa A

Questão 2 - Um prisma de base retangular possui o mesmo volume que um cubo. Sabendo-se que as dimensões do prisma são 6 cm de comprimento, 20 cm de altura e 25 cm de largura, qual é o valor do lado do cubo em centímetros?

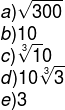
Resolução:

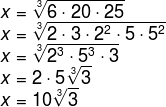
Alternativa D

Por Raul Rodrigues de Oliveira
Professor de Matemática