Média harmônica

A média harmônica é uma dentre as três médias pitagóricas. Utilizamos uma média para representar um conjunto de dados por um único valor. No estudo da estatística, em situações que envolvem grandezas inversamente proporcionais, a média harmônica é a mais interessante para representar esse conjunto. Situações que envolvem densidade, tempo e velocidade, tempo e vazão, entre outras, também podem ser resolvidas com a média harmônica.

Em um conjunto de valores, para calcular a média harmônica, dividimos a quantidade de elementos pela soma do inverso de cada um dos elementos do conjunto.

Leia também: Média, moda e mediana — medidas de tendência centrais

Tópicos deste artigo

• 1 - Resumo sobre média harmônica
• 2 - Videoaula sobre média harmônica
• 3 - O que é média harmônica?
• 4 - Qual a fórmula da média harmônica?
• 5 - Como se calcula a média harmônica?
• 6 - Aplicações da média harmônica
• 7 - Exercícios resolvidos sobre média harmônica

Resumo sobre média harmônica

• A média harmônica é utilizada para representar um conjunto de dados por um único valor.

• Utilizamos a média harmônica para situações envolvendo grandezas inversamente proporcionais.

• Para calcular a média harmônica, utilizamos a fórmula:

Videoaula sobre média harmônica

O que é média harmônica?

No estudo da estatística, a busca por um único valor que facilite o entendimento sobre os dados de um determinado conjunto é bastante recorrente, e para fazer essa representação utilizamos as medidas centrais e as médias. Em determinadas situações, é conveniente utilizarmos a média harmônica entre os dados para representar esse conjunto por um único valor.

Utilizamos a média harmônica quando os dados do conjunto são grandezas inversamente proporcionais, como velocidade e tempo, vazão e tempo, dentre outras situações, sendo ela menos comum que a média aritmética.

Qual a fórmula da média harmônica?

Para obter a média harmônica, calculamos a quantidade de elementos do conjunto dividida pela soma dos inversos desses elementos. Ou seja, dado um conjunto com os elementos (x₁, x₂, x₃,..., x_n), a média harmônica desse conjunto é calculada por:

n → quantidade de elementos

M_h → Média harmônica

Como se calcula a média harmônica?

Para calcular a média harmônica de um conjunto, basta substituirmos os valores na fórmula. Vejamos um caso.

Exemplo

Encontre a média harmônica do conjunto (15, 10, 6).

Resolução:

Temos que n = 3. Substituindo na fórmula:

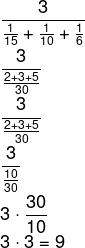
Então, temos que M_h = 9.

Leia também: Média geométrica — uma das três médias pitagóricas

Aplicações da média harmônica

Vejamos algumas aplicações da média harmônica.

Exemplo 1

Para encher um reservatório, há duas torneiras. Uma delas leva 12 horas para encher todo o reservatório e a outra, 8 horas. Caso essas duas torneiras sejam ligadas simultaneamente, qual será o tempo gasto para encher o tanque?

Resolução

Primeiro encontraremos quanto uma torneira demora, em média, para encher o reservatório, calculando a média harmônica dos tempos:

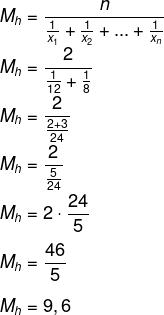
Cada torneira leva em média 9,6 horas para preencher o reservatório, então se ligarmos as duas simultaneamente,

9,6 : 2 = 4,8 horas.

Exemplo 2

Um automóvel fez um percurso com uma velocidade de 100 km/h em determinado dia. Em outro dia, ele fez o mesmo percurso a uma velocidade de 60 km/h. Então, sua velocidade média nesse mesmo percurso seria de quanto?

Resolução

Calculando a média harmônica, temos que:

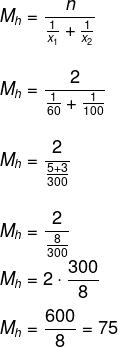
A velocidade média desse automóvel é de 75 km/h.

Leia também: Mediana — uma das medidas de tendência central

Exercícios resolvidos sobre média harmônica

Questão 1

Durante uma viagem espacial, um novo elemento foi descoberto. Ao trazer esse elemento para a Terra, os cientistas perceberam que se tratava de uma mistura totalmente homogênea de três substâncias: substância A, com densidade d = 0,4 g/cm³, substância B, com densidade d = 0,6 g/cm³, e substância C, com densidade d = 1,2 g/cm³. Sabendo que as massas da substância 1 e da substância 2 são as mesmas, então a densidade dessa mistura é de:

a) 0,45 g/cm³

b) 0,55 g/cm³

c) 0,58 g/cm³

d) 0,60 g/cm³

e) 0,65 g/cm³

Resolução

Alternativa D

Para encontrar a densidade, calcularemos a média harmônica desses valores.

Primeiro reescreveremos como fração os números decimais:

Logo, a densidade dessa mistura é de 0,6 g/cm³.

Questão 2

Durante a coleta de dados de uma pesquisa, foram encontrados os números 2, 3, 5, 6 e 9. A média harmônica desses dados

a) está entre 1 e 2.

b) está entre 2 e 3.

c) está entre 3 e 4.

d) está entre 4 e 5.

e) está entre 5 e 6.

Resolução

Alternativa C

Calculando a média harmônica, temos que:

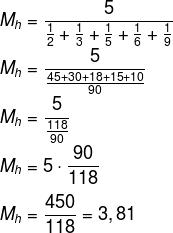
Por Raul Rodrigues de Oliveira
Professor de Matemática