Moda, média e mediana

A moda, a média e a mediana são conhecidas como medidas de tendências centrais. No estudo da Estatística, é bastante comum que elas sejam utilizadas para compreender melhor o comportamento de um conjunto de dados.

Em um conjunto de dados, a moda é o valor mais frequente no conjunto, ou seja, que mais se repete. Já a mediana é o valor central do conjunto. Já com relação às médias, existem vários tipos, sendo as mais comuns a média aritmética simples e a média aritmética ponderada. A moda, a média e a mediana são bastante recorrentes em exames de seleção e no Enem.

Leia também: Medidas de dispersão: amplitude e desvio

Tópicos deste artigo

• 1 - Resumo sobre moda, média e mediana
• 2 - Moda, média e mediana: o que são?
• 3 - Moda
  • Videoaula sobre moda
• 4 - Mediana
  • 1º caso — quantidade ímpar de elementos
  • 2º caso — quantidade par de elementos
  • Videoaula sobre mediana
• 5 - Média
  • Média aritmética simples
  •  Média aritmética ponderada
• 6 - Moda, média e mediana no Enem
• 7 - Exercícios resolvidos sobre moda, média e mediana

Resumo sobre moda, média e mediana

• A moda, a média e a mediana são conhecidas como medidas de tendências centrais.
• Elas são utilizadas para representar um conjunto de dados com um único valor.
• A moda é o valor com maior frequência absoluta em um conjunto.
• A mediana é o valor que está posicionado no centro do conjunto.
• Existem vários tipos de média, mas os principais são a média aritmética simples e a média aritmética ponderada.

Moda, média e mediana: o que são?

A moda, a média e a mediana são conhecidas como medidas de tendências centrais. Durante o estudo da Estatística, utilizamos as medidas centrais para representar um conjunto de dados com um único valor. A partir da moda, da média ou da mediana, é possível tomar determinadas decisões.

Moda

Em um conjunto de dados, a moda é aquele resultado mais recorrente no conjunto, ou seja, com maior frequência absoluta. Já parou para pensar sobre como as lojas planejam os seus estoques de um determinado produto? Ainda que existam várias marcas de um mesmo produto, há aquele tem maior saída. Para analisar isso, é utilizada a moda.

Exemplo:

Em uma loja de calçados femininos, o estoque é reposto mensalmente. Para entender melhor o consumo de seus clientes, o dono da loja decidiu anotar o tamanho escolhido pelos 35 primeiros clientes em uma lista:

N = {35, 37, 36, 34, 38, 35, 37, 37, 33, 36, 38, 37,35, 37, 34, 33, 37, 36, 35, 38, 36, 35, 36, 37, 38, 39, 37, 37, 36, 37, 33, 37, 35, 37, 39}

Analisando os dados coletados, para realizar o próximo pedido, o tamanho de calçado mais recorrente entre as clientes é a moda desse conjunto.

N = {35, 37, 36, 34, 38, 35, 37, 37, 33, 36, 38, 37,35, 37, 34, 33, 37, 36, 35, 38, 36, 35, 36, 37, 38, 39, 37, 37, 36, 37, 33, 37, 35, 37, 39}

A partir da moda, é possível perceber que 37 é o tamanho mais recorrente entre as clientes dessa loja, dado esse que ajudaria a loja na escolha dos tamanhos na hora de repor o estoque.  Representamos a moda por Mo. Nesse caso, temos que Mo = 37.

Para encontrar a moda, basta escolher o valor com maior frequência absoluta.

Exemplo 2:

Analise os conjuntos e encontre a sua moda:

a) A = {1, 0, 2, 3, 1, 4, 5, 1, 2, 3, 0, 7, 8, 9}

Analisando o conjunto A, é possível perceber que existem dois elementos que mais se repetem no conjunto:

A = {1, 0, 2, 3, 1, 4, 5, 1, 0, 3, 0, 7, 8, 9, 0, 1}

Nesse caso existem dois valores que possuem maior frequência absoluta, logo o conjunto terá duas modas, configurando-se como um conjunto bimodal.

Mo = {0, 1}

b) B { 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6}

Analisando esse conjunto, podemos perceber que todos os elementos se repetem de forma igualitária. Quando a frequência absoluta dos termos é a mesma, o conjunto não terá uma moda, logo dizemos que o conjunto é amodal.

• Videoaula sobre moda

Mediana

Dado um conjunto numérico, conhecemos como mediana o valor que ocupa a posição central dos valores quando organizamos esses dados em ordem. Para encontrar a mediana, é possível listar os termos em ordem crescente ou decrescente e encontrar o termo que ocupa a posição central.

Para isso, podemos distinguir dois casos: quando há uma quantidade ímpar de elementos no conjunto e quando há uma quantidade par de elementos no conjunto.

• 1º caso — quantidade ímpar de elementos

Exemplo:

A altura dos professores da área de ciências da natureza de uma escola foi listada a seguir:

A = { 1,79 m; 1,72 m; 1,63 m; 1,82 m; 1,65 m; 1,75 m; 1,80 m}

Para encontrar a mediana, é essencial que o primeiro passo seja colocar os dados em ordem crescente ou decrescente.

A = {1,63; 1,65; 1,72; 1,75; 1,79; 1,80; 1,82}

Note que há sete elementos no conjunto. Como há uma quantidade ímpar de elementos, a mediana será o termo que está exatamente na metade da lista. Para encontrar o termo central, primeiro encontramos a posição desse termo, dividindo a quantidade de termos por 2, e arredondamos o resultado para o próximo número inteiro, que será a posição do termo central.

Como há 7 elementos, sabemos que 7 : 2 = 3,5. Sempre vamos arredondar para o termo posterior, então a mediana desse conjunto é o 4º termo do conjunto. Agora analisaremos o conjunto:

A = {1,63; 1,65; 1,72; 1,75; 1,79; 1,80; 1,82}

Portanto, a mediana é 1,75 m.

• 2º caso — quantidade par de elementos

Quando a quantidade de elementos do conjunto é par, é necessário calcular a média entre os dois termos que se encontram no meio do conjunto em ordem.

Exemplo:

B = { 1, 2, 2, 3, 6, 10, 15, 16,16, 20}

Ao realizar a contagem da quantidade de termos, há 10 termos. Então, temos que 10 : 2 = 5, logo os termos centrais são o 5º e o 6º termo.

• O 5º termo da sequência é 6.
• O 6º termo da sequência é 10.

A mediana é a soma desses números dividida por 2, ou seja, (10 + 6): 2 = 16 : 2 =  8. Logo, a mediana desse conjunto é 8.

• Videoaula sobre mediana

Leia também: Gráficos — representações que facilitam a análise de dados

Média

Entre as medidas centrais, a mais utilizada é a média. Existem vários tipos de média, mas as mais comuns são a média aritmética simples e a média aritmética ponderada.

• Média aritmética simples

A média aritmética é calculada pela soma de todos os elementos do conjunto dividida pela quantidade de elementos do conjunto.

Título: formula-media-artimetica

n → quantidade de elementos

Exemplo:

A idade dos funcionários do departamento de recursos humanos de uma empresa está na lista a seguir:

{28, 30, 29, 31, 32, 33, 34}

Calcule a idade média dos funcionários desse departamento.

Resolução:

Sabemos que há 7 elementos, então temos que:

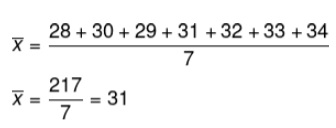
→ Videoaula sobre média aritmética

•  Média aritmética ponderada

Na média aritmética ponderada, são atribuídos pesos para cada um dos valores. Quanto maior for o peso, maior será a influência daquele determinado dado no valor da média aritmética ponderada.

Para calcular a média aritmética ponderada, utilizamos a fórmula:

p₁, p₂, p₃, … p_n → pesos

x₁, x₂, x₃, _… x_n → valores do conjunto

Para calcular a média ponderada, calculamos o produto de cada valor por seu respectivo peso e, depois, calculamos a soma entre esses produtos e dividimos pela soma dos pesos.

Exemplo:

Durante uma seleção de professores, a prova era dividida em algumas etapas, e cada uma delas tinha um peso. O candidato vencedor seria o que alcançasse maior nota. Vamos encontrar, então, o candidato que possui maior média aritmética.

• Prova de língua estrangeira → peso 1
• Prova prática → peso 2
• Prova específica da área→ peso 3
• Análise de currículo → peso 4

Os candidatos Armando e Belchior tiveram as seguintes notas:

Então, calcularemos as médias:

Agora calcularemos a média de Belchior:

O candidato que possui maior média é o Belchior, logo ele será contratado.

→ Videoaula sobre média ponderada

Moda, média e mediana no Enem

A Estatística em si é uma das áreas mais importantes da Matemática e está sempre presente no nosso cotidiano. Tendo isso em vista, em todas as edições da prova do Enem desde 2009, foi comum haver mais de uma questão envolvendo essa área.

A matriz de referências do Enem mostra que um dos objetivos da prova é avaliar a relação do estudante com as medidas centrais.

Isso justifica a recorrência desse conteúdo com problemas ligados a gráficos ou tabelas, nos quais o candidato tem que encontrar uma ou mais medidas centrais para resolver a questão. Vejamos a seguir alguns exercícios resolvidos sobre o tema envolvendo essa habilidade cobrada no Enem.

Exercícios resolvidos sobre moda, média e mediana

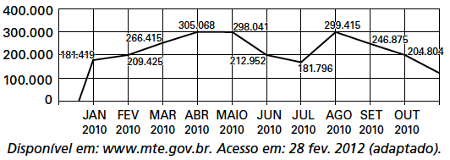
Questão 1 — (Enem 2012) O gráfico apresenta o comportamento de emprego formal surgido, segundo o CAGED, no período de janeiro de 2010 a outubro de 2010.

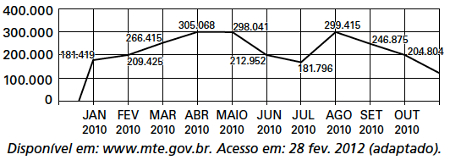
Com base no gráfico, o valor da parte inteira da mediana dos empregos formais surgidos no período é:

A) 212.952

B) 229.913

C) 240.621

D) 255.496

E) 298.041

Resolução:

Alternativa B.

Note que há 10 valores. Quando dividimos 10 por 2, temos que o termo central é a média entre o 5º e o 6º termo da sequência. Colocando a sequência em ordem, temos que:

181.419, 181.719, 204.804, 209.425, 212.952, 246.875, 266.415, 298.041, 299.415, 305.068

(212.952 + 246.875) : 2 = 229.923

Questão 02 — (Enem 2018) A Comissão Interna de Prevenção de Acidentes (CIPA) de uma empresa, observando os altos custos com os frequentes acidentes de trabalho ocorridos, fez, a pedido da diretoria, uma pesquisa do número de acidentes sofridos por funcionários. Essa pesquisa, realizada com uma amostra de 100 funcionários, norteará as ações da empresa na política de segurança no trabalho.

Os resultados obtidos estão no quadro:

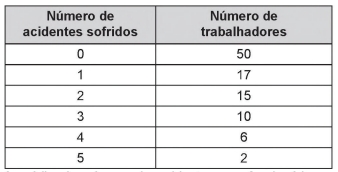
A média do número de acidentes por funcionário na amostra que a CIPA apresentará à diretoria da empresa é:

A) 0,15.

B) 0,30.

C) 0,50.

D) 1,11.

E) 2,22.

Resolução:

Alternativa D.

Calcularemos a média ponderada. Sabendo que o peso será o número de trabalhadores, cuja soma é 100, temos:

Por Raul Rodrigues de Oliveira
Professor de Matemática