Matriz identidade

A matriz identidade é um tipo especial de matriz. Conhecemos como matriz identidade I_n a matriz quadrada de ordem n que possui todos os termos da diagonal iguais a 1 e os termos que não pertencem à diagonal principal iguais a 0. A matriz identidade é considerada o elemento neutro da multiplicação, ou seja, se multiplicamos uma matriz M pela matriz identidade, encontramos como resultado a própria matriz M.

Veja também: O que é o determinante de uma matriz?

Tópicos deste artigo

• 1 - Resumo sobre matriz identidade
• 2 - O que é matriz identidade?
  • ? Tipos de matriz identidade
• 3 - Propriedades da matriz identidade
• 4 - Multiplicação da matriz identidade
• 5 - Exercícios resolvidos sobre matriz identidade

Resumo sobre matriz identidade

• A matriz identidade é a matriz quadrada com elementos da diagonal principal iguais a 1 e com os demais elementos iguais a 0.

• Há matrizes identidade de diversas ordens. Representamos a matriz identidade de ordem n por I _n.

• A matriz identidade é o elemento neutro da multiplicação de matrizes, ou seja, \( A\cdot I_n=A.\)

• O produto entre uma matriz quadrada e sua matriz inversa é a matriz identidade.

O que é matriz identidade?

A matriz identidade é um tipo especial de matriz quadrada. A matriz quadrada é conhecida como matriz identidade se ela possuir todos os elementos da diagonal principal iguais a 1 e os demais elementos iguais a 0. Então, em toda matriz identidade:

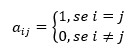
➝ Tipos de matriz identidade

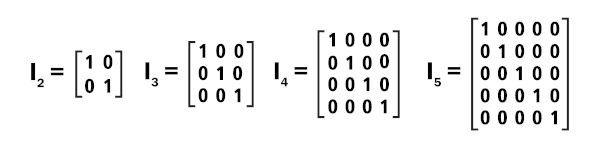
Há matrizes identidade de diversas ordens. A de ordem n é representada por I_n. Vejamos abaixo algumas matrizes de outras ordens.

• Matriz identidade de ordem 1:

\(I_1=\left[1\right]\)

• Matriz identidade de ordem 2:

\(I_2=\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\)

• Matriz identidade de ordem 3:

\(I_3=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)

• Matriz identidade de ordem 4:

\(I_4=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right]\)

• Matriz identidade de ordem 5:

\(I_5=\left[\begin{matrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{matrix}\right]\)

De forma sucessiva, podemos escrever matrizes identidade de diferentes ordens.

Propriedades da matriz identidade

A matriz identidade possui uma importante propriedade, pois ela é o elemento neutro da multiplicação entre as matrizes. Isso significa que qualquer matriz multiplicada pela matriz identidade é igual a ela mesma. Assim, dada a matriz M de ordem n, temos:

\(I_n\cdot M=M\cdot I_n=M\)

Outra propriedade importante da matriz identidade é que o produto entre uma matriz quadrada e sua matriz inversa é a matriz identidade. Dada uma matriz quadrada M de ordem n, o produto de M pela sua inversa é dado por:

\(M\cdot M^{-1}=I_n\)

Leia também: O que é uma matriz triangular?

Multiplicação da matriz identidade

Quando multiplicamos uma matriz M pela matriz identidade de ordem n, obtemos como resultado a matriz M. Vejamos, a seguir, um exemplo do produto da matriz M de ordem 2 pela matriz identidade de ordem 2.

\(A\ =\ \left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right) \) e \(I_n=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)

Supondo que:

\(A\cdot I_n=B\)

Temos:

\(B\ =\left(\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\\\end{matrix}\right)\)

Assim, o produto de A por \(I_n\) será:

\(b_{11}=1\cdot a_{11}\cdot1+0\cdot a_{12}=a_{11}\)

\(b_{12}=0\cdot a_{11}+1\cdot a_{12}=a_{12}\)

\(b_{21}=1\cdot a_{21}+0\cdot a_{22}=a_{21}\)

\(b_{22}=0\cdot a_{21}+1\cdot a_{22}=a_{22}\)

Note que os termos da matriz B são idênticos aos termos da matriz A, ou seja:

\(A\cdot I_n=\left[\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right]=A\)

• Exemplo:

Sendo M a matriz \(M=\ \left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\), calcule o produto entre a matriz M e a matriz \(I_3\).

Resolução:

Realizando a multiplicação, temos:

\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\cdot\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)

\(M\cdot I_3=\left[\begin{matrix}1\ \cdot\ 1\ +\ 0\ \cdot\ 4\ +\ 0\ \cdot\ 0&1\cdot0\ +\ 4\ \cdot\ 1\ +\ 0\cdot\ 0&1\cdot0+4\cdot0+0\cdot1\\2\cdot\ 1\ +\ 5\ \cdot\ 0\ +\ 3\ \cdot\ 0&2\ \cdot\ 0\ +\ 5\cdot1+3\cdot0&2\cdot0+5\cdot0+3\cdot1\\-3\cdot1+\left(-2\right)\cdot0+1\cdot0&-3\cdot0+\left(-2\right)\cdot1+1\cdot0&-3\cdot0+\left(-2\right)\cdot0+1\cdot1\\\end{matrix}\right]\)

\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\)

Exercícios resolvidos sobre matriz identidade

Questão 1

Existe uma matriz quadrada de ordem 3 que é definida por \(a_{ij}=1 \) quando \(i=j\) e \(a_{ij}=0\) e quando \(i\neq j\). Essa matriz é igual a:

A) \( \left[\begin{matrix}1&1&1\\1&1&1\\1&1&1\\\end{matrix}\right]\)

B) \( \left[\begin{matrix}0&0&1\\0&1&0\\1&0&0\\\end{matrix}\right]\)

C) \( \left[\begin{matrix}0&1&1\\0&0&1\\0&0&1\\\end{matrix}\right]\)

D) \( \left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)

E) \( \left[\begin{matrix}1&0&0\\1&1&0\\1&1&1\\\end{matrix}\right]\)

Resolução:

Alternativa D

Analisando a matriz, temos:

\(a_{12}=a_{13}=a_{21}=a_{23}=a_{31}=a_{32}=0\)

\(a_{11}=a_{22}=a_{33}=1\)

Então, a matriz é igual a:

\(\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)

Questão 2

(UEMG) Se a matriz inversa de \(A=\left[\begin{matrix}2&3\\3&x\\\end{matrix}\right]\) é \( \left[\begin{matrix}5&-3\\-3&2\\\end{matrix}\right]\), o valor de x é:

A) 5

B) 6

C) 7

D) 9

Resolução:

Alternativa A

Multiplicando as matrizes, percebemos que o produto delas é igual à matriz identidade. Calculando o produto da segunda linha da matriz pela primeira coluna da sua inversa, temos:

\(3\cdot5+x\cdot\left(-3\right)=0\)

\(15-3x=0\)

\(-\ 3x=0-15\ \)

\(-\ 3x=-\ 15\)

\(x=\frac{-15}{-3}\)

\(x=5\ \)

Por Raul Rodrigues de Oliveira
Professor de Matemática