Um fato muito discutido é a utilização dos conceitos de matrizes e determinantes nas provas de vestibulares. Quanto a isto, é necessário estudar e compreender de quais maneiras esses conceitos costumam ser cobrados nas diversas provas de vestibular.
A parte de matrizes é bem extensa, pois possui um sistema aritmético diferenciado e particular entre outros novos conceitos que são utilizados apenas no grupo numérico das matrizes. Portanto, é importante que se compreenda os conceitos aritméticos (adição, subtração, multiplicação), consequências provindas do sistema aritmético (matriz transposta, matriz inversa) e os determinantes de matrizes, conceitos estes que podem ser estudados na seção Matriz e Determinante.
Algo que se observa nas provas de vestibulares é que as matrizes são minoria nas questões e quando aparecem no vestibular são cobrados, em uma só questão, quase todos os conceitos sobre matrizes. Nesse artigo, mostraremos como essas questões são abordadas e veremos como relacionar os conceitos de matrizes em uma só questão.
Devemos nos atentar para a concepção das questões que são abordadas quanto a sua interdisciplinaridade que corrobora com a aplicação em um contexto real. Portanto, iremos nos deparar com questões que necessitam de uma interpretação e compreensão do enunciado de modo que consigamos determinar o que deve ser respondido e quais informações o enunciado oferece.
Questão 1) (Faap-SP) Uma montadora produz três modelos de veículos, A, B e C. Neles podem ser instalados dois tipos de air bags, D e E. A matriz [air bag modelo] mostra a quantidade de unidades de air bags instaladas:

Numa determinada semana foram produzidas as seguintes quantidades de veículos, dadas pela matriz :
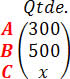
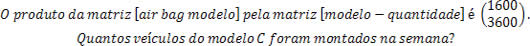
a) 300 c) 150 e) 100
b) 200 d) 0
Resolução: A questão envolve três matrizes, uma matriz que relaciona a quantidade de air bags em cada um dos três modelos produzidos pela fábrica, a matriz que informa a quantidade de carros produzidos por semana, e a matriz produto dessas duas matrizes citadas.
O objetivo final é determinar a quantidade de carros do modelo C, montados durante a semana. Esta quantidade está expressa pela incógnita x. Para determinar o valor da incógnita x, devemos montar essa equação matricial.
Para praticidade na notação, denotaremos da seguinte forma as matrizes:
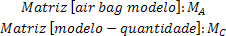
Sendo assim, temos a seguinte expressão:
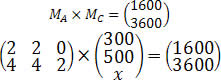
Nesse momento, devemos compreender os conceitos de equações matriciais – estes conceitos necessitam da compreensão das operações aritméticas das matrizes e de igualdade de matrizes.
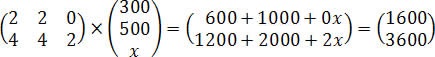
Note que a primeira linha corresponde à quantidade de carros produzidos com o air bag do tipo D; e a segunda linha, à quantidade de carros produzidos com air bag do tipo E. Contudo, veja que nenhum carro do modelo C foi fabricado utilizando o air bag D. Com isso, basta determinarmos a quantidade de carros do modelo C com o air bag E, ou seja, utilizaremos a segunda linha.
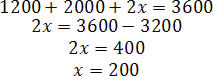
2) (UEL – PR) Uma das formas de se enviar uma mensagem secreta é por meio de códigos matemáticos, seguindo os passos:
1. Tanto o destinatário quanto o remetente possuem uma matriz chave C;
2. O destinatário recebe do remetente uma matriz P, tal que MC=P, onde M é a matriz mensagem a ser decodificada;
3. Cada número da matriz M corresponde a uma letra do alfabeto: 1=a, 2=b, 3=c, ..., 23=z;
4. Consideremos o alfabeto com 23 letras, excluindo as letras, k, w e y.
5. O número zero corresponde ao ponto de exclamação.
6. A mensagem é lida, encontrando a matriz M, fazendo correspondência número/letra e ordenando as letras por linhas da matriz conforme segue: m11m12m13m21m22m23m31m32m33.
Considere as matrizes:
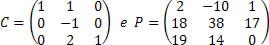
Com base nos conhecimentos e nas informações descritas, assinale a alternativa que apresenta a mensagem que foi enviada por meio da matriz M.
a) Boasorte! b) Boaprova! c) Boatarde!
d) Ajudeme! e) Socorro!
Resolução: Devemos nos atentar para a equação matricial que codifica/decodifica a mensagem. MC=P, ela será a base para os nossos cálculos.
As matrizes C e P foram informadas, a matriz M é o que queremos descobrir, portanto determinaremos seus elementos como incógnitas iguais ao que foi informado no sexto passo dado no enunciado.
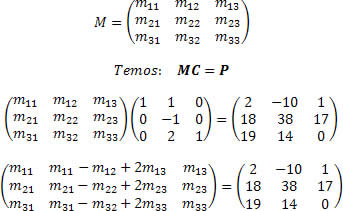
Igualando os elementos das duas matrizes conseguiremos obter os valores dos elementos da matriz M.
m11=2; m12= 14; m13=1; m21=18; m22=14; m23=17; m31=19; m32=5; m33=0.
Transpondo para letras obtemos: Boasorte!
Veja que, por mais que sejam muitos os conceitos abordados, necessita-se de atenção nas operações entre matrizes, pois são diversas operações ao mesmo tempo. Tendo cuidado e organização, questões envolvendo matrizes não serão um empecilho no seu vestibular.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola