A condição de alinhamento de três pontos é o método que utilizamos para verificar se três pontos são colineares ou não colineares. Dizemos que os pontos são colineares se eles estão alinhados, ou seja, se existe uma reta que passa por esses três pontos, eles são colineares.
Leia também: O que é distância entre dois pontos?
Tópicos deste artigo
- 1 - O que são pontos colineares e pontos não colineares?
- 2 - Como saber se três pontos são colineares?
- 3 - Exercícios resolvidos sobre condição de alinhamento de três pontos
O que são pontos colineares e pontos não colineares?
→ Pontos colineares
Ao representar três pontos no plano cartesiano, conhecemos como pontos colineares os que estão alinhados, ou seja, são três pontos que pertencem a uma mesma reta.
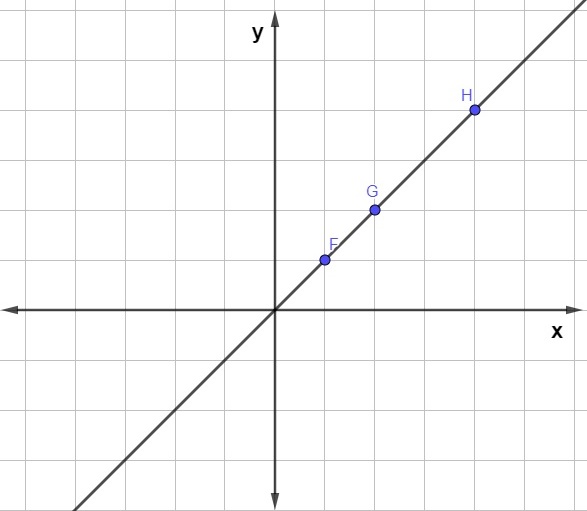
→ Pontos não colineares
Ao representar três pontos no plano cartesiano, quando não existe uma reta que os contém, dizemos que eles são não colineares.
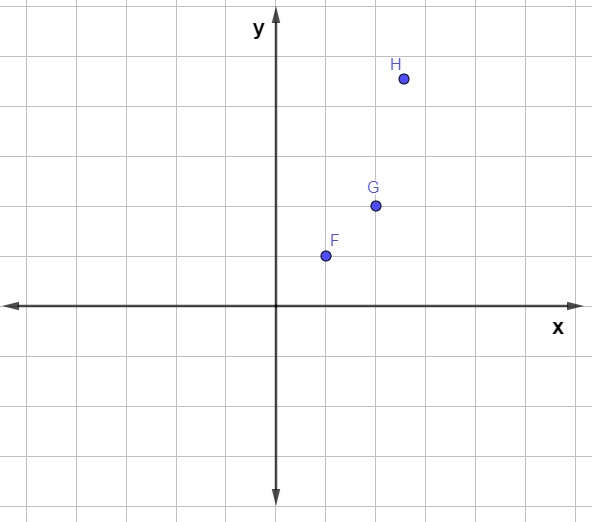
Como saber se três pontos são colineares?
Para sabermos se os três pontos estão ou não alinhados, verificamos se eles satisfazem a condição de alinhamento de três pontos. Para saber se os três pontos são colineares, primeiro construímos a matriz em que os elementos da primeira e segunda coluna são as coordenadas x e y de cada ponto, e a última coluna possui termos igual a 1. Dados três pontos de coordenadas P1x1,y1, P2x2,y2 e P3x3,y3, se esses três pontos estão alinhados, eles serão colineares se:
\(det(A)=\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\\\end{matrix}\right|=0\ \)
Caso o determinante det(A) seja diferente de 0, então esses pontos são ditos não colineares.
Exemplo 1
Verifique se os pontos A(3, 2), B(4, 4) e C(5, 6) são colineares.
Resolução
Para verificar se esses pontos são colineares, primeiro montaremos o determinante da matriz, substituindo cada linha pela abcissa e a ordenada de cada ponto:
\(det(A)=\left|\begin{matrix}3&2&1\\4&4&1\\5&6&1\\\end{matrix}\right|\ \)
Calculando o det(A), temos que:
\(det\left(A\right)=3\cdot4\cdot1+2\cdot1\cdot5+1\cdot4\cdot6-1\cdot4\cdot5-3\cdot1\cdot6-2\cdot4\ \cdot1\)
\(det\left(A\right)=12+10+24-20-18-8\)
\(det\left(A\right)=46-46\)
\(det\left(A\right)=0\)
Como det(A) = 0, então os pontos A, B e C são colineares.
Exemplo 2
Verifique se os pontos D(1, 4), E(2, 1) e F(5, 5) estão alinhados.
Resolução
Montando o determinante, temos que:
\(det(A)=\left|\begin{matrix}1&4&1\\2&1&1\\5&5&1\\\end{matrix}\right|\ \)
Calculando o determinante:
\(det\left(A\right)=1\cdot1\cdot1+4\cdot1\cdot5+1\cdot2\cdot5-1\cdot1\cdot5-1\cdot1\cdot5-4\cdot2\cdot1\)
\(det\left(A\right)=1+20+10-5-5-8\)
\(det\left(A\right)=31-18\)
\(det(A)=13\)
Podemos afirmar que os pontos D, E e F não são colineares.
Veja também: Condição de concorrência de duas retas — qual é?
Exercícios resolvidos sobre condição de alinhamento de três pontos
Questão 1
Os pontos A(1, 2), B(3, 8) e C(t, 0) são colineares. Nessas condições, podemos afirmar que o valor de t é:
A) 1/2
B) 1/3
C) 5/3
D) 7/2
E) 2/5
Resolução:
Alternativa B
Montando o determinante, temos que:
\(det(A)=\left|\begin{matrix}1&2&1\\3&8&1\\t&0&1\\\end{matrix}\right|\ \)
Calculando o determinante:
\(det\left(A\right)=1\cdot8\cdot1+2\cdot1\cdot t+1\cdot3\cdot0-1\cdot8\cdot t-1\cdot1\cdot0-2\cdot3\cdot1\)
\(det\left(A\right)=8+2t+0-8t-0-6\)
\(det\left(A\right)=-6t+2\)
Sabemos que det(A) = 0, logo, temos que:
\(-6t+2=0\)
\(-6t=-\ 2\)
\(t=\frac{2}{6}\)
Simplificando a fração, temos que:
\(t=\frac{1}{3}\)
Questão 2
Sobre a condição de alinhamentos de três pontos, podemos afirmar que:
I. Três pontos são sempre colineares.
II. Três pontos colineares são pontos que pertencem a uma mesma reta.
III. Se os pontos \(P_1\left(x_1,y_1\right),\ P_2\left(x_2,y_2\right)\ e\ P_3\left(x_3,y_3\right)\) são colineares, então:
\(\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\\\end{matrix}\right|\neq0\ \)
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são verdadeiras.
E) Somente a afirmativa I é falsa.
Resolução:
Alternativa B
I. Três pontos são sempre colineares. (Falso)
Nem sempre os pontos são colineares.
II. Três pontos colineares são pontos que pertencem a uma mesma reta. (Verdadeiro)
III. Se os pontos \(P_1\left(x_1,y_1\right),\ P_2\left(x_2,y_2\right)\ e\ P_3\left(x_3,y_3\right)\) são colineares, então: \(\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\\\end{matrix}\right|\neq0\) (Falso)
Para que os pontos sejam colineares, é necessário que o determinante seja igual a zero, e não diferente de zero.
Por Raul Rodrigues de Oliveira
Professor de Matemática