PUBLICIDADE
A ordem de grandeza é um método matemático para arredondamento por meio do qual transformamos um número em uma potência de base 10. Para conseguirmos isso, primeiramente o representamos em notação científica.
Cada ordem de grandeza recebe uma nomenclatura e símbolo. Por exemplo, para números em milhão, a representação é \({10}^6 \) e a nomenclatura é mega. No caso das escalas das ordens de grandeza do comprimento, por exemplo, elas dependem exclusivamente do valor da ordem de grandeza da medida de comprimento obtida.
Veja também: Radiciação — a operação matemática que é inversa à potenciação
Tópicos deste artigo
- 1 - Resumo sobre ordem de grandeza
- 2 - O que é ordem de grandeza?
- 3 - Regras para ordem de grandeza
- 4 - Como saber a ordem de grandeza de um número?
- 5 - Prefixos e símbolos das ordens de grandezas
- 6 - Exercícios resolvidos sobre ordem de grandeza
Resumo sobre ordem de grandeza
-
Ordem de grandeza é a análise dos números que estão em potência de base 10. Para fazermos essa análise, usamos a notação científica.
-
A notação científica se dá quando reduzimos um número de vários algarismos a um número entre 1 e 9, com o produto de potência de base 10.
-
Se o número for menor que 3,16, a ordem de grandeza é a potência encontrada. Mas se for maior ou igual a 3,16, então a ordem de grandeza é a potência somada a um. Ou seja, para sabermos a ordem de grandeza, precisamos transformar o número em notação científica e analisar a qual regra ele se encaixa.
-
As escalas das ordens de grandeza do comprimento se referem às nomenclaturas das medidas quanto à sua ordem de grandeza. São elas: subatômica, atômica, escala humana e astronômica.
O que é ordem de grandeza?
A ordem de grandeza se dá quando expressamos um número na potência de base 10 mais próxima a ele. É muito empregada quando queremos demonstrar medidas de maneira mais reduzida.
→ Notação científica
Para expressarmos um número na potência de base 10 mais próxima a ele, primeiramente o representamos na notação científica. Notação científica é a escrita de números com muitos algarismos em potência de 10.
Para transformarmos o número em notação científica, podemos seguir os passos abaixo:
-
Andamos com a vírgula até que o número fique entre 1 e 9.
-
Escrevemos esse número o multiplicando por uma potência de base 10.
-
Contamos quantas casas a vírgula foi movida. Esse será o valor da potência.
-
Se a vírgula foi movida da esquerda para a direita, a potência é elevada a um valor negativo. Se a vírgula foi movida da direita para a esquerda, a potência é elevada a um valor positivo.
-
Exemplo:
Qual é a forma do número 5.760.000 em notação científica?
Resolução:
Seguindo os passos aprendidos, transformaremos o número. Situando-o entre 1 e 9:
5,760
Multiplicando-o por uma potência de 10:
\(5,760\bullet{10}^n\)
O valor \(n\ \) se refere à quantidade de movimentos da vírgula. Como a movemos em 6 casas, então \(n=6\):
\(5,760\bullet{10}^{\pm6}\)
E como a vírgula foi movida da direita para a esquerda, a potência é positiva:
\(5,760\bullet{10}^6\)
Então, 5.760.000 em notação científica é \(5,760\bullet{10}^6.\)
-
Videoaula sobre notação científica
Regras para ordem de grandeza
As regras para encontrarmos a ordem de grandeza são:
-
Transformar o número em notação científica.
-
Analisar posteriormente:
-
Se o número for menor que 3,16, a ordem de grandeza é a própria potência de 10.
-
Se o número for maior ou igual a 3,16, a ordem de grandeza é a potência de 10 somando 1 ao expoente.
Como saber a ordem de grandeza de um número?
Para sabermos a ordem de grandeza de um número, é necessário seguir as regras estabelecidas para tal. Transformamos o número em notação científica e conseguimos determinar seu valor.
Por exemplo, a ordem de grandeza do número 20 é \({10}^1\), porque se transformarmos esse número em notação científica teremos \(2\bullet{10}^1\), além de 2 ser menor que 3,16. Já se quisermos saber a ordem de grandeza do número 590, temos que transformá-lo, da mesma maneira, em notação científica, obtendo \(5,9\bullet{10}^2\). Contudo 5,9 é maior que 3,16, então a sua ordem de grandeza é \({10}^2\) somando 1 ao expoente. Para o número 590, portanto, a ordem de grandeza é \({10}^3\).
Saiba mais: Grandezas vetoriais e escalares — grandezas que dependem de diferentes informações para serem definidas
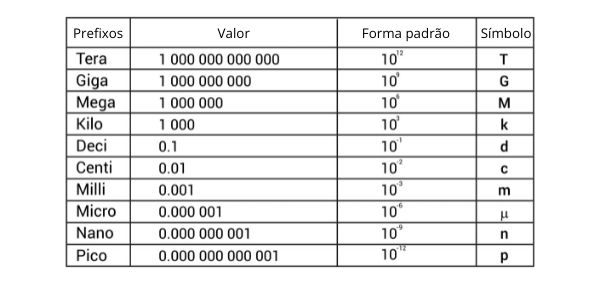
Prefixos e símbolos das ordens de grandezas
Dependendo da ordem de grandeza com a qual lidamos, há prefixos e símbolos específicos para a potência de 10 em questão, conforme podemos ver na tabela abaixo:
Escala das ordens de grandeza do comprimento
A nomenclatura das escalas de comprimento varia de acordo com a ordem de grandeza dos números, como podemos ver abaixo.
-
Subatômico: a medida varia de 0 até a ordem de \({10}^{-15}\) (ordem dos femtômetros). Serve para os quarks, elétrons etc.
-
Atômico: varia de \({10}^{-15}\) até a ordem de \(\ {10}^{-6}\) (ordem dos micrômetros). Serve para os prótons, átomos de hidrogênio, vírus etc.
-
Escala humana: varia de \({10}^{-6}\) até a ordem de \( {10}^6\) (ordem dos megametros). Serve para os cabelos, carros, edifícios etc.
-
Astronômico: varia de \({10}^6\) até o \(\infty\). Serve para os planetas, estrelas, galáxias etc.
Exercícios resolvidos sobre ordem de grandeza
Questão 1
(UFPE) Em um hotel com 200 apartamentos o consumo médio de água por apartamento é de 100 litros por dia. Qual a ordem de grandeza do volume que deve ter o reservatório do hotel, em metros cúbicos, para abastecer todos os apartamentos durante um dia?
A) \({10}^1\)
B) \({10}^2\)
C) \({10}^3\)
D) \({10}^4\)
E) \({10}^5\)
Resolução:
Alternativa A
Primeiramente, calcularemos o consumo total do dia:
\(200\bullet100=20000\ litros\)
Para transformar litros em \(m^3\), faremos uma regra de três:
\(1m^3\ — 1000 l\)
\(x\ — 20 000 l\)
O volume em \(m^3\) é \(20\ l\). Em notação científica, temos \(2\bullet{10}^1\). Como 2 é menor que 3,16, a ordem de grandeza é \({10}^1\).
Questão 2
(UFPI) A nossa galáxia, a Via Láctea, contém cerca de 400 bilhões de estrelas. Suponha que 0,05% dessas estrelas possuam um sistema planetário onde exista um planeta semelhante à Terra. O número de planetas semelhantes à Terra, na Via Láctea, é:
A) \( 2·{10}^{4}\)
B) \( 2·{10}^{6}\)
C) \( 2·{10}^{8}\)
D) \( 2·{10}^{11}\)
E) \( 2·{10}^{12}\)
Resolução:
Alternativa C
De início, faremos a multiplicação para encontrar o número de planetas semelhantes à Terra:
Então, existem 200.000.000 possíveis “Terras”. Transformando o valor em notação científica:
\(200\ 000\ 000=2\bullet{10}^8\)
Por Pâmella Raphaella Melo
Professora de Física
