Vamos imaginar que presenciamos uma colisão frontal entre um muro e um automóvel popular que se move com uma velocidade pequena. Nessa colisão, vimos que o carro recuou um pouco no momento da batida. Mas se ao invés de um carro fosse um ônibus, com mesma velocidade, provavelmente presenciaríamos a destruição do muro e veríamos também que o ônibus continuaria avançando instantes após a colisão.
Voltando à situação inicial, se o carro estiver se movendo com uma velocidade relativamente grande e colidir com o muro, podemos dizer que seu movimento depois da colisão será um pouco diferente do que o da situação anterior. O carro poderá então destruir o muro; e também, após a colisão, poderá continuar seu movimento. Dessa forma, podemos concluir que para certa massa, a quantidade de movimento é maior para velocidades maiores.
Associamos uma orientação à descrição dos movimentos que surgem acoplados. Por exemplo, um nadador empurra a água para trás e avança para frente. Nesse caso, estamos afirmando que a velocidade do nadador tem uma direção e um sentido enquanto a velocidade da porção de água empurrada tem a mesma direção, mas sentido oposto.
Nos exemplos mencionados acima, buscamos indícios que nos permitem afirmar que a quantidade de movimento dos sistemas permanece constante, durante o tempo em que ocorreu a interação, isto é, do instante imediatamente anterior até o instante imediatamente posterior à colisão.
A maioria das colisões, entretanto, não é frontal. Em um jogo de sinuca, por exemplo, uma bola pode colidir com outra bola um pouco de lado ou de raspão, e as duas se afastam em direções diferentes. Contudo, mesmo nessas situações, a quantidade de movimento do sistema se conserva.
Por sua generalidade, a conservação da quantidade de movimento no sistema é um dos princípios fundamentais da Física, utilizado para calcular a velocidade de recuo das armas, para projetar foguetes espaciais, máquinas industriais, etc.
Consideremos um corpo de massa m que, em determinado instante, possui velocidade v em relação a um dado referencial. Denominamos quantidade de movimento ou momento linear desse corpo a grandeza vetorial dada pelo produto da massa (m) do corpo pela sua velocidade (v), no referencial adotado. Matematicamente, definimos a quantidade de movimento Q com o produto
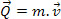
Dessa maneira, podemos concluir que o valor de Q tem as seguintes características:
- direção: coincidente com a direção da velocidade v
- sentido: igual ao da velocidade v (pois m é positivo)
- módulo: Q = m.v
- unidade no SI: = kg.m.s-1
Por Domiciano Marques
Graduado em Física
