A proporção áurea ou proporção divina é uma igualdade associada a ideias de harmonia, beleza e perfeição. Euclides de Alexandria, matemático grego que viveu por volta de 300 a.C., foi um dos primeiros pensadores a formalizar esse conceito que até hoje intriga pesquisadores de diversas áreas.
O motivo desse interesse é que a proporção áurea pode ser observada de maneira aproximada na natureza, inclusive nas sementes e folhas de plantas e no corpo humano. Consequentemente, a proporção áurea é objeto de estudo de diferentes profissionais, como biólogos, arquitetos, artistas e designers.
Leia também: Número pi — uma das constantes mais importantes da Matemática
Tópicos deste artigo
- 1 - Resumo sobre proporção áurea
- 2 - Como calcular o número de ouro?
- 3 - Proporção áurea e a sequência de Fibonacci
- 4 - Proporção áurea e o retângulo de ouro
- 5 - Aplicações da proporção áurea
- 6 - Exercícios resolvidos sobre proporção áurea
Resumo sobre proporção áurea
-
A proporção áurea é a proporção para \(a>b>0\) tal que
\(\frac{a+b}a =\frac{a}b\)
-
Nessas condições, a razão \(\frac{a}b\) é denominada razão áurea.
-
A proporção áurea está conectada a concepções de equilíbrio, pureza e perfeição.
Não pare agora... Tem mais depois da publicidade ;) -
A letra grega ϕ (lê-se: fi) representa o número de ouro, que é a constante obtida a partir da proporção áurea.
-
Na sequência de Fibonacci, os quocientes entre cada termo e seu antecessor se aproximam do número de ouro.
-
O retângulo áureo é um retângulo cujos lados estão em razão áurea.
O que é proporção áurea?
Considere um segmento de reta dividido em dois pedaços: o maior de medida a e o de menor medida b. Perceba que a+b é a medida de todo o segmento.

A proporção áurea é a igualdade entre as razões \(\mathbf{\frac{a+b}a}\) e \(\mathbf{\frac{a}{b}}\), ou seja
\(\frac{a+b}a =\frac{a}b\)
Nesse contexto, dizemos que a e b estão em razão áurea.
Mas para quais valores de a e b temos a proporção áurea? É o que veremos a seguir.
Como calcular o número de ouro?
A razão \(\frac{a}b\) (ou, do mesmo modo, a razão \(\frac{a+b}a\)) resulta em uma constante chamada de número de ouro e representada pela letra grega ϕ. Assim, é comum escrevermos
\(\frac{a+b}a =\frac{a}b=ϕ\)
Para calcular o número de ouro, vamos considerar a proporção áurea para b = 1. Assim, podemos facilmente encontrar o valor de a e obter ϕ a partir da igualdade \(\mathbf{\frac{a}{b}=ϕ}\).
Observe que podemos escrever a proporção áurea da seguinte maneira, utilizando a propriedade de multiplicação cruzada:
\(a^2=b⋅(a+b)\)
Substituindo b = 1, temos que
\(a^2=1⋅(a+1)\)
\(a^2-a-1=0\)
Aplicando a fórmula de Bhaskara para essa equação do segundo grau, concluímos que a solução positiva de a é
\(a=\frac{1+\sqrt5}2\)
Como a é medida de um segmento, vamos desconsiderar a solução negativa.
Portanto, como \(\frac{a}b=ϕ\), o valor exato do número de ouro é:
\(ϕ=\frac{1+\sqrt5}2\)
Calculando o quociente, obtemos o valor aproximado do número de ouro:
\(ϕ≈1,618033989\)
Veja também: Como resolver operações matemáticas com frações?
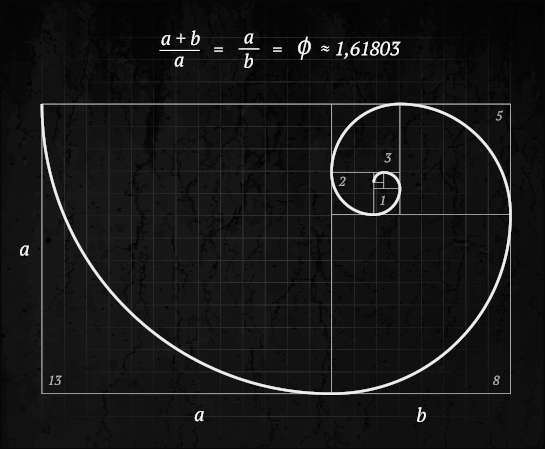
Proporção áurea e a sequência de Fibonacci
A sequência de Fibonacci é uma lista de números em que cada termo, a partir do terceiro, é igual à soma dos dois antecessores. Vejamos os dez primeiros termos dessa sequência:
\(a_1=1\)
\(a_2=1\)
\(a_3=1+1=2\)
\(a_4=1+2=3\)
\(a_5=2+3=5\)
\(a_6=3+5=8\)
\(a_7=5+8=13\)
\(a_8=8+13=21\)
\(a_9=13+21=34\)
\(a_{10}=21+34=55\)
À medida que calculamos o quociente entre cada termo e seu antecessor da sequência de Fibonacci, vamos nos aproximando do número de ouro ϕ:
\(\frac{a_2}{a_1}=\frac{1}1=1\)
\(\frac{a_3}{a_2}=\frac{2}1=2\)
\(\frac{a_4}{a_3}=\frac{3}2=1,5\)
\(\frac{a_5}{a_4}=\frac{5}3=1,6666…\)
\(\frac{a_6}{a_5}=\frac{8}5=1,6\)
\(\frac{a_7}{a_6}=\frac{13}8=1,625\)
\(\frac{a_8}{a_7}=\frac{21}{13}=1,6153…\)
\(\frac{a_9}{a_8}=\frac{34}{21}=1,61904…\)
\(\frac{a_10}{a_9}=\frac{55}{34}=1,61764…\)
Proporção áurea e o retângulo de ouro
Um retângulo em que o lado maior a e o lado menor b estão em razão áurea é chamado de retângulo de ouro. Um exemplo de retângulo de ouro é o retângulo cujos lados medem 1 cm e \(\frac{1+\sqrt5}2\) cm.
Saiba mais: O que são grandezas diretamente proporcionais?
Aplicações da proporção áurea
Note que, até agora, estudamos a proporção áurea apenas em contextos matemáticos abstratos. A seguir, veremos alguns exemplos aplicados, mas é necessário cuidado: a proporção áurea não se apresenta de maneira exata em nenhum desses casos. O que existem são análises de contextos diversos em que o número de ouro aparece de forma aproximada.
-
Proporção áurea na Arquitetura
Alguns estudos afirmam que estimativas do número de ouro são observadas em certas relações das dimensões da Pirâmide de Quéops, no Egito, e do prédio sede da ONU, em Nova Iorque.

-
Proporção áurea no corpo humano
As medidas do corpo humano variam de uma pessoa para outra, e não há um tipo de corpo perfeito. No entanto, ao menos desde a Grécia Antiga, há debates acerca de um corpo matematicamente ideal (e totalmente inatingível na realidade), com medidas relacionadas à proporção áurea. Nesse contexto teórico, por exemplo, a razão entre a altura de uma pessoa e a distância entre seu umbigo e o chão seria o número de ouro.
-
Proporção áurea na arte
Há pesquisas sobre as obras “O Homem Vitruviano” e “Mona Lisa”, do italiano Leonardo da Vinci, que sugerem o uso de retângulos áureos.

-
Proporção áurea na natureza
Existem estudos que apontam uma relação entre a proporção áurea e o modo com que as folhas de certas plantas se distribuem em um caule. Esse arranjo das folhas é chamado de filotaxia.

-
Proporção áurea no Design
A proporção áurea também é estudada e empregada na área de Design como uma ferramenta na composição de projetos.

Exercícios resolvidos sobre proporção áurea
Questão 1
(Enem) Um segmento de reta está dividido em duas partes na proporção áurea quando o todo está para uma das partes na mesma razão em que essa parte está para a outra. Essa constante de proporcionalidade é comumente representada pela letra grega ϕ, e seu valor é dado pela solução positiva da equação ϕ2 = ϕ+1.
Assim como a potência \(ϕ^2\), as potências superiores de ϕ podem ser expressas da forma \(aϕ+b\), em que a e b são inteiros positivos, como apresentado no quadro.

A potência \(ϕ^7\), escrita na forma aϕ+b (a e b são inteiros positivos), é
a) 5ϕ+3
b) 7ϕ+2
c) 9ϕ+6
d) 11ϕ+7
e) 13ϕ+8
Resolução
Como \(ϕ^7=ϕ⋅ϕ^6\), temos que
\(ϕ^7=ϕ⋅ϕ^6 = ϕ⋅(8ϕ+5)\)
Aplicando a distributiva,
\(ϕ^7=8ϕ^2+5ϕ\)
Como \(ϕ^2=ϕ+1\),
\(ϕ^7=8⋅(ϕ+1)+5ϕ\)
\(ϕ^7=13ϕ+8\)
Alternativa E.
Questão 2
Classifique cada afirmação abaixo sobre o número de ouro em V (verdadeira) ou F (falsa).
I. O número de ouro ϕ é irracional.
II. Os quocientes entre cada termo e seu antecessor na sequência de Fibonacci se aproximam do valor de ϕ.
III. 1,618 é o arredondamento com três casas decimais do número de ouro ϕ.
A sequência correta, de cima para baixo, é
a) V-V-V
b) F-V-F
c) V-F-V
d) F-F-F
e) F-V-V
Resolução
I. Verdadeira.
II. Verdadeira.
III. Verdadeira.
Alternativa A.
Fontes
FRANCISCO, S.V. de L. Entre o fascínio e a realidade da razão áurea. Dissertação (Mestrado Profissional em Matemática em Rede Nacional) – Instituto de Biociências, Letras e Ciências Exatas, Universidade Estadual Paulista Júlio de Mesquita Filho. São Paulo, 2017. Disponível em: http://hdl.handle.net/11449/148903.
SALES, J. da S. A proporção áurea presente na natureza. Trabalho de Conclusão de Curso (Licenciatura em Matemática), Instituto Federal de Educação, Ciência e Tecnologia do Piauí. Piauí, 2022. Disponível em http://bia.ifpi.edu.br:8080/jspui/handle/123456789/1551.
Por Maria Luiza Alves Rizzo
Professora de Matemática