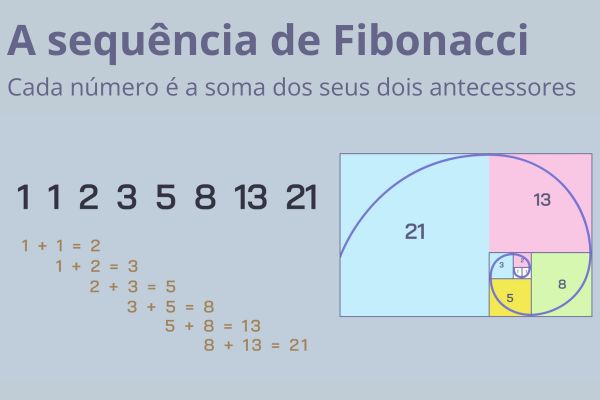
A sequência de Fibonacci é uma sequência numérica em que cada termo a partir do terceiro é a soma dos dois antecessores. O primeiro termo da sequência de Fibonacci é o número 1 e o segundo termo também é o número 1. O terceiro termo é 2, pois 1+1=2. Já o quarto termo é 3, pois 1+2=3. E assim sucessivamente.
Estudos sugerem que essa sequência foi atribuída a Fibonacci por causa de uma situação-problema em um de seus livros sobre a reprodução de uma população de coelhos.
Leia também: Progressões — o que são, diferença entre PA e PG
Tópicos deste artigo
- 1 - Resumo sobre a sequência de Fibonacci
- 2 - Qual é a sequência de Fibonacci?
- 3 - Fórmula de Fibonacci
- 4 - Sequência de Fibonacci, proporção áurea e o número de ouro
- 5 - Sequência de Fibonacci e o retângulo de ouro
- 6 - Exemplos da sequência de Fibonacci na natureza
- 7 - Quem foi Leonardo Fibonacci?
Resumo sobre a sequência de Fibonacci
- A sequência de Fibonacci é uma sequência numérica infinita em que cada termo a partir do terceiro é a soma dos dois termos anteriores.
- Portanto, a sequência de Fibonacci é \(\left(1,1,2,3,5,8,13,21,34,55\ldots\right)\)
- Formalmente, a sequência de Fibonacci é dada por
\(F_1=1\)
\(F_2=1\)
\(F_n=F_{n-1}+F_{n-2} , n\geq3\)
- A razão entre termos consecutivos da sequência de Fibonacci \(\left(\frac{F_n}{F_{n-1}}\right)\) se aproxima do número de ouro para valores crescentes de n.
Qual é a sequência de Fibonacci?
Vamos representar cada termo da sequência de Fibonacci pela letra F. Assim, Fn é o termo que está na posição n.
O primeiro termo da sequência de Fibonacci é 1 e o segundo termo da sequência de Fibonacci também é 1. Do terceiro termo em diante, devemos somar os dois termos anteriores para construir a sequência. Isso significa que o terceiro termo é 2, pois 1+1=2.
Portanto, os dez primeiros termos da sequência de Fibonacci são
\(F_1=1\)
\(F_2=1\)
\(F_3=2\)
\(F_4=1+2=3\)
\(F_5=2+3=5\)
\(F_6=3+5=8\)
\(F_7=5+8=13\)
\(F_8=8+13=21\)
\(F_9=13+21=34\)
\(F_{10}=21+34=55\)
E assim sucessivamente. Perceba que essa sequência é infinita e crescente. Utilizando a notação de sequência, expressamos a sequência de Fibonacci por
\(\left(1,1,2,3,5,8,13,21,34,55\ldots\right)\)
Observação: Alguns autores consideram que o primeiro termo da sequência de Fibonacci é o 0. Assim, alguns artigos podem apresentar a sequência de Fibonacci como (0,1,1,2,3,5,8,13...). Neste texto vamos adotar F1=1.
Veja também: Como calcular proporções
Fórmula de Fibonacci
Cada termo na posição n, a partir de n=3, é a soma entre os dois termos anteriores, que ocupam as posições n-1 e n-2. Portanto, podemos representar cada termo Fn da sequência de Fibonacci da seguinte maneira:
\(F_n=F_{n-1}+F_{n-2} , n\geq3\)
Sequência de Fibonacci, proporção áurea e o número de ouro
O número de ouro é uma constante obtida a partir da proporção áurea. Esse número, representado pela letra grega ϕ, é igual a \(\frac{1+\sqrt5}{2}\). Um valor aproximado para o número de ouro é 1,618034.
Existe uma fórmula, chamada fórmula de Binet, que pode ser utilizada para encontrar qualquer termo da sequência de Fibonacci. Essa fórmula é dada pela seguinte expressão, com n≥1:
\(F_n=\frac{1}{\sqrt5}\left(\frac{1+\sqrt5}{2}\right)^n-\frac{1}{\sqrt5}\left(\frac{1-\sqrt5}{2}\right)^n\)
Essa expressão pode ser escrita em função do número de ouro:
\(F_n=\frac{\phi^n-\left(-\phi\right)^{-n}}{\sqrt5}\)
Além disso, para valores crescentes de n, a razão entre um termo da sequência de Fibonacci e seu antecessor se aproxima do número de ouro. Observe alguns exemplos:
\(\frac{F_2}{F_1}=\frac{1}{1}=1\)
\(\frac{F_3}{F_2}=\frac{2}{1}=2\)
\(\frac{F_4}{F_3}=\frac{3}{2}=1,5\)
\(\frac{F_5}{F_4}=\frac{5}{3}\approx1,667\)
\(\frac{F_6}{F_5}=\frac{8}{5}=1,6\)
\(\frac{F_7}{F_6}=\frac{13}{8}=1,625\)
\(\frac{F_8}{F_7}=\frac{21}{13}\approx1,615\)
Sequência de Fibonacci e o retângulo de ouro
Um retângulo em que as medidas dos lados estão em razão áurea é chamado de retângulo de ouro ou retângulo áureo. Isso significa que, nesse tipo de retângulo, a razão entre o lado maior e o menor é igual ao número de ouro.
A imagem abaixo apresenta uma composição de quadrados cujas medidas dos lados são os primeiros termos da sequência de Fibonacci. Note que inicialmente foram colocados dois quadrados de lado 1, um ao lado do outro. Em seguida, foi posicionado um quadrado de lado 2, depois um quadrado de lado 3, depois um de lado 5 e assim por diante.
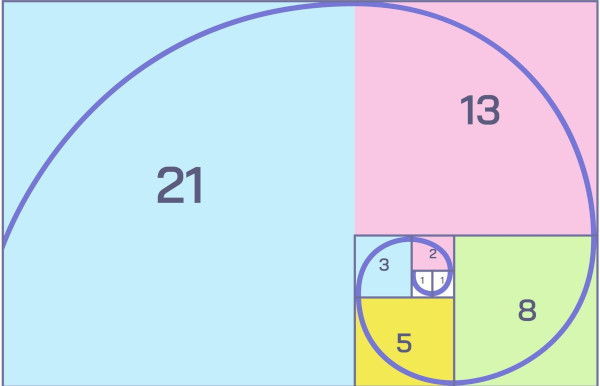
Se continuarmos infinitamente com essa construção, pela relação entre a sequência de Fibonacci e o número de ouro, teremos formado um retângulo de ouro.
Saiba mais: Qual é o valor de pi?
Exemplos da sequência de Fibonacci na natureza
Há estudos que indicam que as quantidades de pétalas em algumas flores são os termos da sequência de Fibonacci. Além disso, considerando a relação com o número de ouro, pode-se observar de maneira aproximada a sequência de Fibonacci na distribuição das folhas de certas plantas.
Quem foi Leonardo Fibonacci?

Leonardo de Pisa, também conhecido como Leonardo Fibonacci, foi um matemático italiano nascido no final do século XII. Filho de um renomado comerciante, Fibonacci viajou por diversos países da Europa, África e Oriente Médio, onde teve contato com outras culturas e técnicas matemáticas. Suas contribuições foram registradas em livros sobre Aritmética, Álgebra, Geometria e Trigonometria.
Fontes
C.Q.D. - Revista Eletrônica Paulista de Matemática, Bauru, v. 18, 2020. Disponível em: https://sistemas.fc.unesp.br/ojs/index.php/revistacqd/article/view/211
OLIVEIRA, J. J. de. Sequências de Fibonacci: Possibilidades de Aplicação no Ensino Básico. Dissertação (Mestrado Profissional em Matemática) – Universidade Federal da Bahia. Salvador, 2013. Disponível em: https://repositorio.ufba.br/handle/ri/22821
SILVA, R. L.; ALMEIDA, R. L. da S. A fantástica sequência de Fibonacci e o enigmático número de ouro: contexto histórico, definições, propriedades e aplicações.