Progressão Aritmética (PA)

A progressão aritmética (PA) é uma sequência numérica que utilizamos para descrever o comportamento de certos fenômenos na matemática. Em uma PA, o crescimento ou decrescimento é sempre constante, isto é, de um termo para o outro, a diferença será sempre a mesma, e essa diferença é conhecida como razão.

Como consequência do comportamento previsível de uma progressão, é possível descrevê-la a partir de uma fórmula conhecida como termo geral. Por esse mesmo motivo, é possível também calcular a soma dos termos de uma PA utilizando uma fórmula específica.

Leia também: Progressão geométrica – como calcular?

Tópicos deste artigo

• 1 - O que é uma PA?
• 2 - Tipos de progressões aritméticas
  • Crescente
  • Decrescente
  • Constante
• 3 - Propriedades de uma PA
  • 1ª propriedade
  • 2ª propriedade
• 4 - Soma dos termos de uma PA
• 5 - Interpolação de meios aritméticos
• 6 - Exercícios resolvidos

O que é uma PA?

Entendendo que uma PA é uma sequência de termos em que a diferença entre um termo e o seu anterior é sempre constante, para descrever essa progressão a partir de uma fórmula, precisamos encontrar o termo inicial, ou seja, o primeiro termo de uma progressão, e a sua razão, que é essa diferença constante entre os termos.

De modo geral, a PA é escrita da seguinte forma:

(a₁, a₂,a₃, a₄,a₅, a₆,a₇, a₈)

O primeiro termo é o a₁ e, a partir dele, ao somar a razão r, vamos encontrar o termos sucessor.

a₁ + r = a₂
a₂ + r = a₃
a₃ + r = a₄

...

Logo, para escrever a progressão aritmética, precisamos saber quem é o seu primeiro termo e qual a sua razão.

Exemplo:

Vamos escrever os seis primeiros termos de uma PA sabendo que seu primeiro termo é 4 e sua razão é igual a 2. Conhecendo a₁ =4 e r = 2, concluímos que essa progressão começa em 4 e vai aumentando de 2 em 2. Sendo assim, podemos descrever os seus termos.

a₁ = 4

a₂ = 4+ 2 = 6

a₃ = 6 + 2 = 8

a₄ = 8 + 2 = 10

a₅= 10 + 2 = 12

a₆ = 12 + 2 =14

Essa PA é igual a (4,6,8,10,12,14 …).

Termo geral de uma PA

Descrever a PA a partir de uma fórmula facilita que encontremos qualquer um dos seus termos. Para encontrar um termo qualquer de uma PA, utilizamos a seguinte fórmula:

N→ é a posição do termo;

a₁→ é o primeiro termo;

r → razão.

Exemplo:

Encontre o termo geral da PA (1,5,9,13,…) e o 5º, 10º e 23º termo.

1º passo: encontrar a razão.

Para encontrar a razão, basta calcular a diferença entre dois termos consecutivos: 5 – 1 = 4; então, nesse caso, r = 4 .

2º passo: encontrar o termo geral.

Como sabemos que a₁= 1 e r = 4, vamos substituir na fórmula.

a_n=a₁ + r (n - 1)

a_n=1 + 4 (n - 1)

a_n=1 + 4n - 4  

a_n= 4n – 3 → termo geral da PA

3º passo: conhecendo o termo geral, vamos calcular o 5º, 10º e 23º termo.

5º termo → n = 5
a_n=4n – 3
a₅=4·5 – 3
a₅=20 – 3
a₅=17

10º termo → n = 10
a_n=4n – 3
a₁₀=4·10 – 3
a₁₀=40 – 3
a₁₀=37

23º termo → n = 23
a_n=4n – 3
a₂₃=4·23 – 3
a₂₃=92 – 3
a₂₃=89

Tipos de progressões aritméticas

Existem três possibilidades para uma PA. Ela pode ser crescente, decrescente ou constante.

• Crescente

Como o nome sugere, uma progressão aritmética é crescente quando, à medida que os termos vão aumentando, o valor deles também aumenta, ou seja, o segundo termo é maior que o primeiro, o terceiro é maior que o segundo e assim sucessivamente.

a₁ < a₂ < a₃ < a₄ < …. n

Para que isso aconteça, a razão precisa ser positiva, ou seja, uma PA é crescente se r > 0.

Exemplos:

(2,3,4,5,6,7,8,9 …)
(0,5,10,15,20,25...)

• Decrescente

Como o nome sugere, uma progressão aritmética é decrescente quando, à medida que os termos vão aumentando, o valor deles vai diminuindo, ou seja, o segundo termo é menor que o primeiro, o terceiro é menor que o segundo e assim sucessivamente.

a₁ > a₂ > a₃ > a₄ > …. >a_n

Para que isso aconteça, a razão precisa ser negativa, ou seja, uma PA é crescente se r < 0.

Exemplos:

(10,9,8,7,6,5,4,3,2, …)
(0, -5, -10, -15, -20, …)

• Constante

Uma progressão aritmética é constante quando, à medida que os termos vão aumentando, o valor continua o mesmo, ou seja, o primeiro termo é igual ao segundo, que é igual ao terceiro e assim sucessivamente.

a₁ = a₂ = a₃ = a₄ = …. =a_n

Para que uma PA seja constante, a razão precisa ser igual a zero, ou seja, r = 0.

Exemplos:

(1,1,1,1,1,1,1….)
(-2, -2 -2, -2, …)

Veja também: Produto dos termos de uma PG – qual é a fórmula?

Propriedades de uma PA

• 1ª propriedade

Dado um termo qualquer de uma PA, a média aritmética entre seu sucessor e antecessor é igual a esse termo.

Exemplo:

Considere a progressão (-1, 2 , 5, 8, 11) e o termo 8. A média entre 11 e 5 é igual a 8, ou seja, a soma do sucessor com o antecessor de um número na PA sempre é igual a esse número.

• 2ª propriedade

A soma de termos equidistantes é sempre igual.

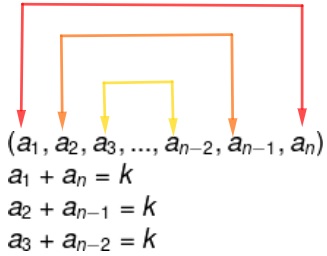
Exemplo:

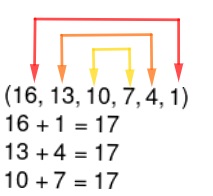
Soma dos termos de uma PA

Suponha que queiramos somar os seis termos da PA mostrada anteriormente: (16,13,10,7,4,1). Podemos simplesmente somar os seus termos – nesse caso em que há poucos termos, é possível –, mas se for uma sequência maior, convém utilizar a propriedade. Sabemos que a soma de termos equidistantes é sempre igual, como vimos na propriedade, então, se realizarmos essa soma uma vez e multiplicarmos pela metade da quantidade de termos, teremos a soma dos seis primeiros termos da PA.

Note que, no exemplo, estaríamos calculando a soma do primeiro com o último, que é igual a 17, multiplicada pela metade da quantidade de termos, ou seja, 17 vezes 3, que é igual a 51.

A fórmula da soma dos termos de uma PA foi desenvolvida pelo matemático Gauss, que percebeu essa simetria nas progressões aritméticas. A fórmula é escrita da seguinte forma:

S_n → soma dos n elementos

a₁ → primeiro termo

a_n → último termo

n → quantidade de termos

Exemplo:

Calcule a soma dos números ímpares de 1 até 2000.

Resolução:

Sabemos que essa sequência é uma PA (1,3,5, …. 1997, 1999). Realizar a soma seria bastante trabalhoso, logo a fórmula é bastante conveniente. De 1 até 2000, metade dos números são ímpares, logo há 1000 números ímpares.

Dados:

n→ 1000

a₁ → 1

a_n → 1999

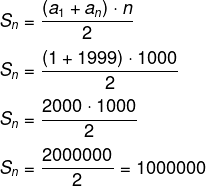
Acesse também: Soma de uma PG finita – como fazer?

Interpolação de meios aritméticos

Conhecendo dois termos não consecutivos de uma progressão aritmética, é possível encontrar todos os termos que estão entre esses dois números, o que conhecemos como interpolação de meios aritméticos.

Exemplo:

Vamos interpolar 5 meios aritméticos entre 13 e 55. Isso significa que há 5 números entre 13 e 55 e que eles formam uma progressão.

(13, ___,___,___,___,___, 55).

Para encontrar esses números, é necessário encontrar a razão. Conhecemos o primeiro termo (a₁ = 13) e também o 7º termo (a₇= 55), mas sabemos que:

a_n = a₁ + r ·(n – 1 )

Quando n = 7 → a_n= 55. Também conhecemos o valor de a₁=13. Assim, substituindo na fórmula, temos que:

55 = 13 + r ·( 7 – 1 )

55 = 13 + 6r

55 – 13 = 6r

42 = 6r

r = 42:6

r = 7.

Conhecendo a razão, podemos encontrar os termos que estão entre 13 e 55.

13 + 7 = 20

21 + 7 = 27

28 + 7 = 34

35 + 7 = 41

41 + 7 = 49

(13, 20, 27, 34, 41, 49, 55)

Exercícios resolvidos

Questão 1 - (Enem 2012) - Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.

A quantidade de cartas que forma o monte é:

A) 21.
B) 24.
C) 26.
D) 28.
E) 31.

Resolução

Alternativa B.

Primeiro vamos calcular o total de cartas que foram usadas. Estamos trabalhando com uma PA cujo primeiro termo é 1 e a razão também é 1. Então, calculando a soma das 7 fileiras, o último termo é 7 e o valor de n também é 7.

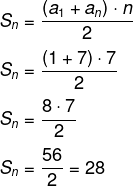
Sabendo que o total de cartas usadas foram 28 e que há 52 cartas, o monte é formado por:

52 – 28 = 24 cartas

Questão 2 - (Enem 2018) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea que se inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros da praça, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de 20 metros entre os postes, até que o último poste seja colocado a uma distância de 1.380 metros da praça.

Se a prefeitura pode pagar, no máximo, R$ 8.000,00 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é:

A) R$512 000,00.
B) R$520 000,00.
C) R$528 000,00.
D) R$552 000,00.
E) R$584 000,00.

Resolução

Alternativa C.

Sabemos que serão colocados postes de 20 em 20 metros, ou seja, r = 20, e que o primeiro termo dessa PA é 80. Além disso, sabemos que o último termo é 1380, porém, não sabemos quantos termos existem entre 80 e 1380. Para calcular essa quantidade n de termos, vamos utilizar a fórmula do termo geral.

Dados: a_n = 1380; a₁=80; e r = 20.

a_n=a₁ + r·(n-1)

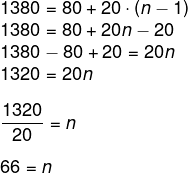
Serão colocados 660 postes. Se cada um custará no máximo R$ 8.000, o maior valor que poderá ser gasto com a colocação desses postes é:

66· 8 000 = 528 000