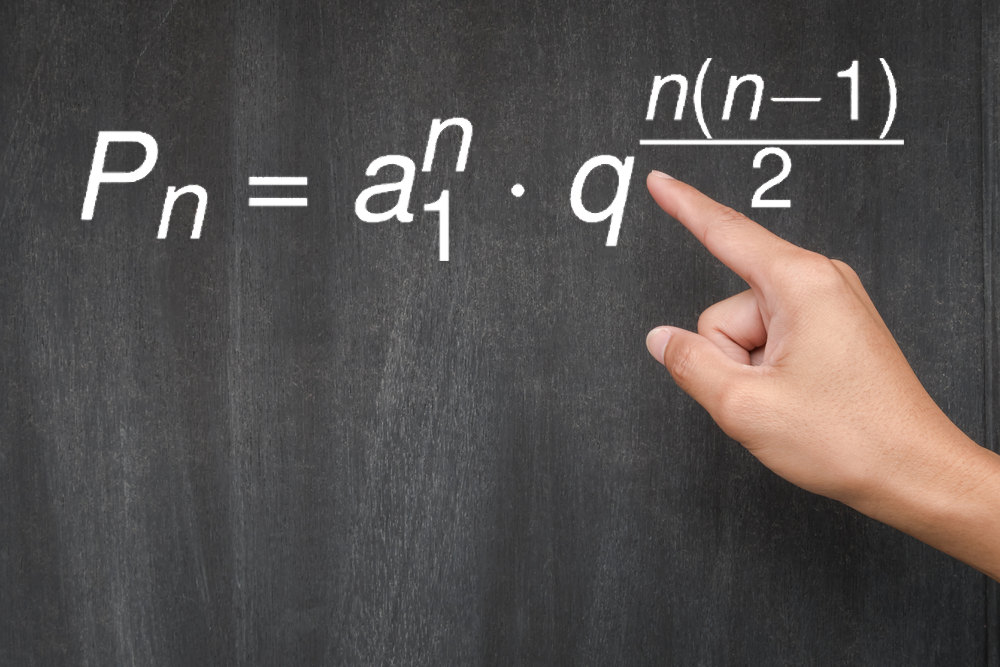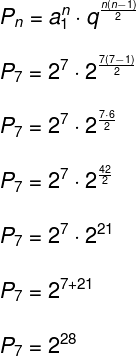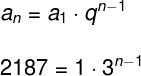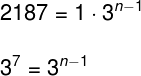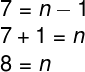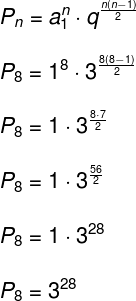Produto dos termos de uma PG

A fórmula do produto dos termos de uma progressão geométrica (PG) é uma fórmula matemática usada para encontrar o resultado da multiplicação entre todos os termos de uma PG e é dada pela seguinte expressão:
 

Nessa fórmula, P_n é o produto dos termos da PG, a₁ é o primeiro termo e está elevado a n na fórmula. Além disso, q é a razão da PG e n é o número de termos que serão multiplicados.

Como o número de termos a ser multiplicado é finito, então essa fórmula só é válida para os n primeiros termos da PG ou para progressões geométricas finitas.

Veja também: Soma dos temos de uma PG finita

Tópicos deste artigo

• 1 - Exercícios resolvidos
• 2 - Exercício 1
• 3 - Exercício 2

Exercícios resolvidos

Exercício 1

Calcule o produto dos termos da PG (2, 4, 8, 16, 32, 64, 128).

Observe que essa PG possui 7 termos, o primeiro deles é 2 e a razão também é 2, pois 4 : 2 = 2. Substituindo esses valores na fórmula do produto dos termos da PG, teremos:
 

O último passo, em que escrevemos 2^{7 + 21} = 2²⁸, foi feito por meio das propriedades de potências.

Exercício 2

Determine o produto dos termos da PG finita a seguir: (1, 3, 9, … 2187).

A razão dessa PG é 3 : 1 = 3, seu primeiro termo é 1, seu último termo é 2187, mas o número de termos que ela possui é desconhecido. Para encontrá-lo, será necessário usar a fórmula do termo geral da PG, presente na imagem a seguir. Substituindo os valores conhecidos nessa fórmula, teremos:
 

Como 2187 = 3⁷, teremos:
 

Como as bases das potências obtidas são iguais, podemos igualar seus expoentes:
 

Assim, o número de termos dessa PG é 8. Substituindo razão, primeiro termo e número de termos na fórmula do produto dos termos da PG, teremos:
 

Veja também: Soma dos termos de uma PG infinita

Por Luiz Paulo Silva
Graduado em Matemática