O estudo das progressões está pautado nas sequências que possuem um padrão matemático. De acordo com este padrão é possível determinar diversos elementos de uma sequência apenas sabendo seu primeiro elemento e a razão dessa sequência.
Em determinadas situações é necessário calcularmos a somatória dos termos de uma determinada sequência. Nas sequências do tipo de progressão geométrica, podemos encontrar dois tipos de somatória, a somatória de termos finitos e a somatória de termos infinitos - Soma dos Termos de uma PG Infinita . Veremos então a expressão para calcularmos a soma de finitos termos de uma P.G, utilizando apenas o termo a1 e a razão q.
Sendo assim, vejamos a demonstração da expressão da Soma da P.G. finita.
Seja (a1, a2, …, an) uma P.G, na qual sua razão é: q ≠ 1
Portanto, a expressão que representa a soma destes n termos é dada da seguinte forma:
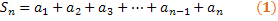
Façamos uma multiplicação por q em toda a expressão, ou seja, devemos multiplicar os dois lados da igualdade:

Façamos a subtração da expressão (2) pela expressão (1):
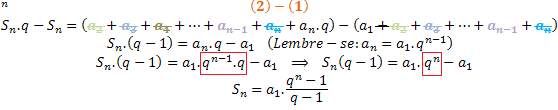
Veja que para utilizarmos esta expressão, devemos ter uma razão diferente de 1.
Vale ressaltar que poderíamos ter subtraído a expressão 1 da expressão 2. Se fizermos isto, iremos obter a seguinte expressão:
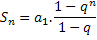
Com isso basta aprendermos a utilizar estas expressões (que são iguais, cabe a você decidir qual utilizar) para resolvermos questões que envolvem esse conceito.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe BrasilEscola
