Os gráficos são representações que facilitam a análise de dados, os quais costumam ser dispostos em tabelas quando se realiza pesquisas estatísticas. Eles trazem muito mais praticidade, principalmente quando os dados não são discretos, ou seja, quando são números consideravelmente grandes. Além disso, os gráficos também apresentam de maneira evidente os dados em seu aspecto temporal.
Leia também: O que é a margem de erro em uma pesquisa?
Tópicos deste artigo
Elementos do gráfico
Ao construirmos um gráfico em estatística, devemos levar em consideração alguns elementos que são essenciais para sua melhor compreensão. Um gráfico deve ser simples devido à necessidade de passar uma informação de maneira mais rápida e coesa, ou seja, em um gráfico estatístico, não deve haver muitas informações, devemos colocar nele somente o necessário.
As informações em um gráfico devem estar dispostas de maneira clara e verídica para que os resultados finais sejam dados de modo coeso com a finalidade da pesquisa.
Tipos de gráficos
Em estatística é muito comum a utilização de diagramas para representar dados, diagramas são gráficos construídos em duas dimensões, isto é, no plano. Existem vários modos de representá-los, as principais são: gráfico de pontos, gráfico de linha, gráfico de barra, gráfico de coluna e gráfico de setor.
Leia mais: Moda, média e mediana: números que resumem informações de listas de dados
-
Gráfico de pontos
Também conhecido como Dotplot, é utilizado quando possuímos uma tabela de distribuição de frequência, sendo ela absoluta ou relativa. O gráfico de pontos tem por objetivo apresentar os dados das tabelas de forma resumida e que possibilite a análise das distribuições desses dados.
Exemplo
Suponha uma pesquisa, realizada em uma escola de educação infantil, na qual foram coletadas as idades das crianças. Nessa coleta foi organizado o seguinte rol:
Rol: {1, 1, 2, 2, 2, 2, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 6}
Podemos organizar esses dados utilizando um Dotplot
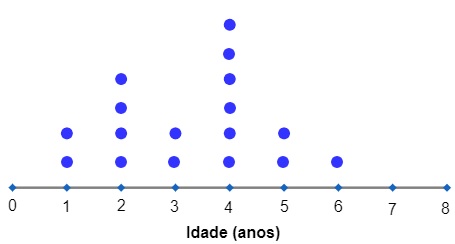
Observe que a quantidade de pontos corresponde à frequência de cada idade e o somatório de todos os pontos fornece-nos a quantidade total de dados coletados.
-
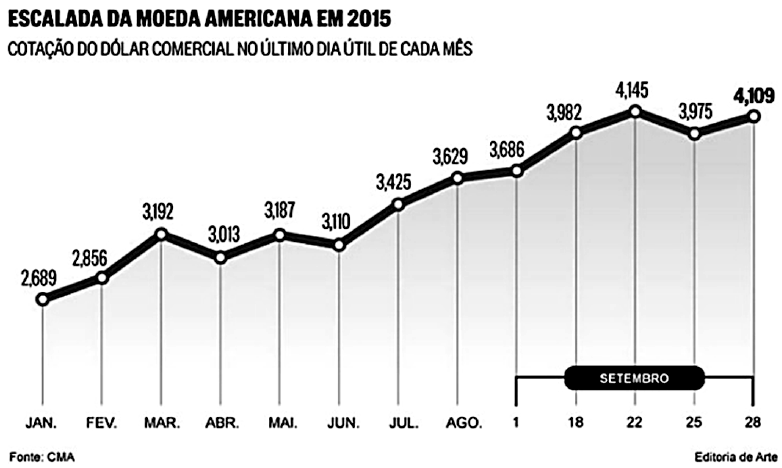
Gráfico de linha
É utilizado em casos que existe a necessidade de analisar dados ao longo do tempo, esse tipo de gráfico é muito presente em análises financeiras. O eixo das abscissas (eixo x) representa o tempo, que pode ser dado em anos, meses, dias, horas etc., enquanto o eixo das ordenadas (eixo y) representa o outro dado em questão.
Uma das vantagens desse tipo de gráfico é a possibilidade de realizar a análise de mais de uma tabela, por exemplo.
Exemplo
Uma empresa deseja verificar seu faturamento em determinado ano, os dados foram dispostos em uma tabela:
|
Mês |
Faturamento |
Mês |
Faturamento |
|
Janeiro |
R$ 10.000,00 |
0 |
R$ 8.000,00 |
|
Fevereiro |
R$ 15.000,00 |
0 |
R$ 16.000,00 |
|
Março |
R$ 8.000,00 |
0 |
R$ 10.000,00 |
|
Abril |
R$ 15.000,00 |
0 |
R$ 11.000,00 |
|
Maio |
R$ 20.000,00 |
0 |
R$ 11.000,00 |
|
Junho |
R$ 24.000,00 |
0 |
R$ 20.000,00 |
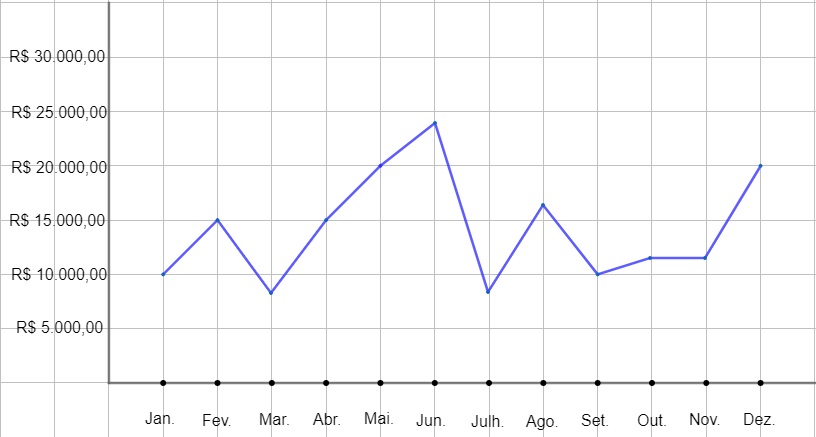
Veja que nesse tipo de gráfico é possível ter uma melhor noção a respeito do crescimento ou do decrescimento dos rendimentos da empresa.
-
Gráfico de barras
Tem como objetivo comparar os dados de determinada amostra utilizando retângulos de mesma largura e altura. Altura essa que deve ser proporcional ao dado envolvido, isto é, quanto maior a frequência do dado, maior deve ser a altura do retângulo.
Exemplo
Imagine que determinada pesquisa tem por objetivo analisar o percentual de determinada população que acesse ou tenha: internet, energia elétrica, rede celular, aparelho celular ou tablet. Os resultados dessa pesquisa podem ser dispostos em um gráfico como este:
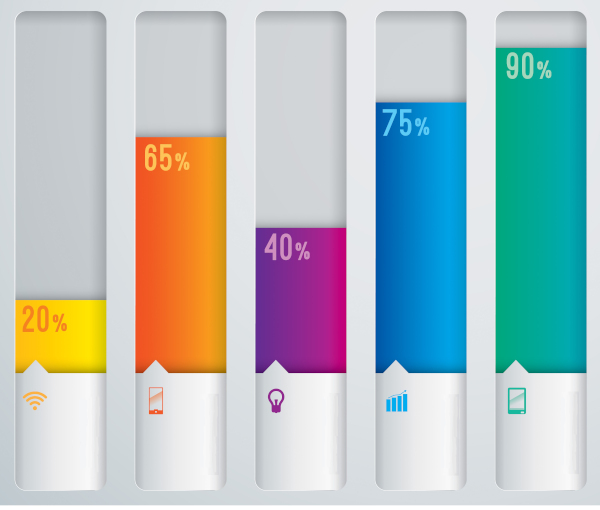
-
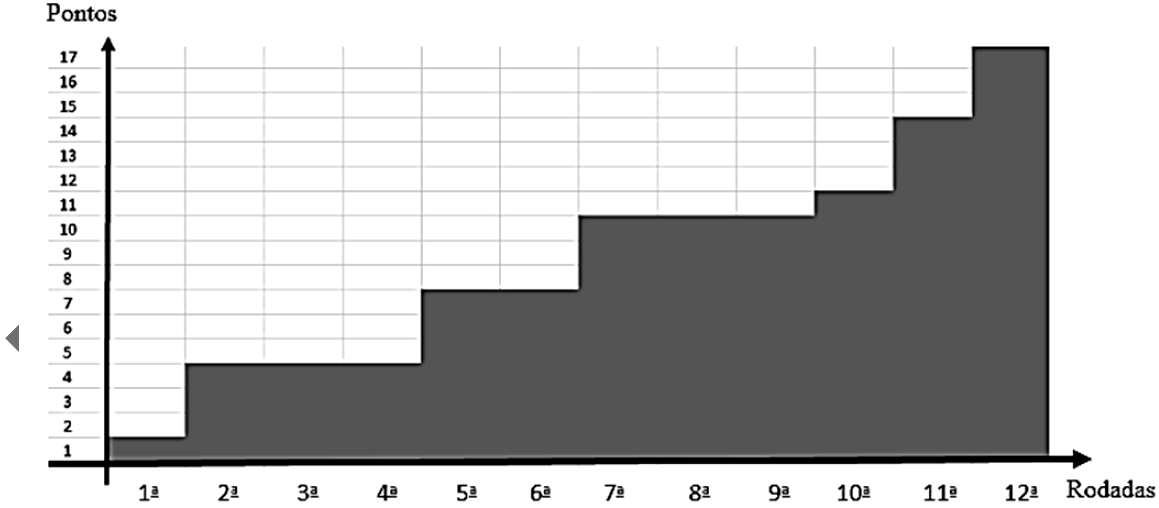
Gráfico de colunas
Seu estilo é semelhante ao do gráfico de barras, sendo utilizado para a mesma finalidade. O gráfico de colunas então é usado quando as legendas forem curtas, a fim de não deixar muitos espaços em branco no gráfico de barra.
Exemplo
Este gráfico está, de forma genérica, quantificando e comparando determinada grandeza ao longo de alguns anos.
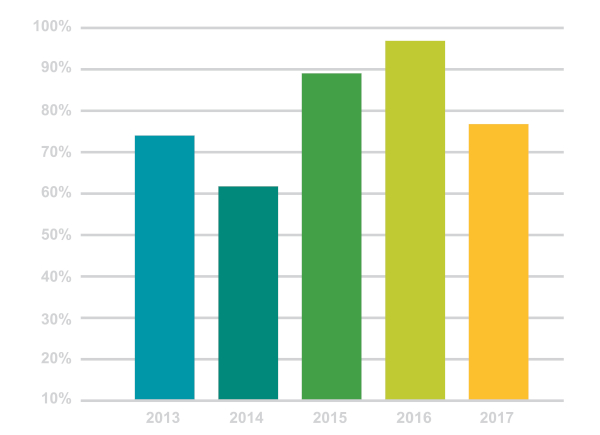
-
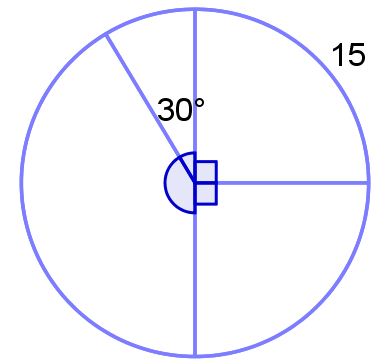
Gráfico de setor
É utilizado para representar dados estatísticos com um círculo dividido em setores, as áreas dos setores são proporcionais às frequências dos dados, ou seja, quanto maior a frequência, maior a área do setor circular.
Exemplo
Este exemplo, de forma genérica, está apresentando diferentes variáveis com frequências diversas para determinada grandeza, a qual pode ser, por exemplo, a porcentagem de votação em candidatos em uma eleição.
Leia também: Área do setor circular: como calcular
Exercícios resolvidos
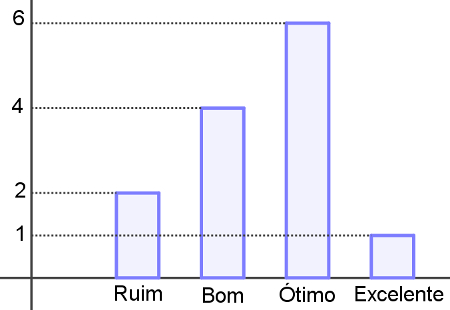
Questão 1 – (Fuvest - 1999) A distribuição das idades dos alunos de uma classe é dada pelo seguinte gráfico:
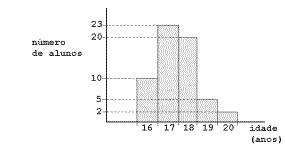
Qual das alternativas representa melhor a média de idade dos alunos?
a) 16 anos e 10 meses
b) 17 anos e 1 mês
c) 17 anos e 5 meses
d) 18 anos e 6 meses
e) 19 anos e 2 meses
Solução
Alternativa c.
Note que o eixo x do gráfico fornece-nos a idade dos alunos e o eixo y fornece-nos a frequência de cada uma das idades, ou seja, a quantidade de vezes que a idade aparece. Assim, devemos utilizar a média ponderada para calcular a média das idades.
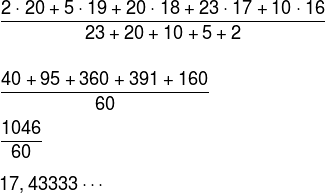
Sabemos que 17,43333… = 17 + 0,4333… . Para transformar 0,43333… em meses devemos multiplicá-lo por 12, logo:
0,4333 · 12 = 5 meses
Portanto, a média de idade desses alunos é de 17 anos e 5 meses.
Por Robson Luiz
Professor de Matemática