Medidas de dispersão: variância e desvio padrão

No estudo da Estatística, dispomos de algumas estratégias para verificar se os valores apresentados em um conjunto de dados estão dispersos ou não e o quão distantes um do outro eles podem estar. As ferramentas empregadas para que isso seja possível são classificadas como medidas de dispersão e denominadas de variância e desvio padrão. Vejamos o que representa cada uma delas:

Variância:

• Dado um conjunto de dados, a variância é uma medida de dispersão que mostra o quão distante cada valor desse conjunto está do valor central (médio).

• Quanto menor é a variância, mais próximos os valores estão da média; mas quanto maior ela é, mais os valores estão distantes da média.

• Considere que x₁, x₂, …, x_n são os n elementos de uma amostra e que x é a média aritmética desses elementos. O cálculo da variância amostral é dado por:

  Var. amostral = (x₁ – x)² + (x₂ – x)² + (x₃ – x)² + ... + (x_n – x)²
                        ​n – 1

• Se, em contrapartida, quisermos calcular a variância populacional, consideraremos todos os elementos da população, e não apenas de uma amostra. Nesse caso, o cálculo possui uma pequena diferença. Observe:

  Var. populacional = (x₁ – x)² + (x₂ – x)² + (x₃ – x)² + ... + (x_n – x)²
                             n

Desvio Padrão:

• O desvio padrão é capaz de identificar o “erro” em um conjunto de dados, caso quiséssemos substituir um dos valores coletados pela média aritmética.

• O desvio padrão aparece junto à média aritmética, informando o quão “confiável” é esse valor. Ele é apresentado da seguinte forma:

  média aritmética (x) ± desvio padrão (dp)

• O cálculo do desvio padrão é feito a partir da raiz quadrada positiva da variância. Portanto:

  dp = √var

Vamos agora aplicar o calculo da variância e do desvio padrão em um exemplo:

Em uma escola, a direção decidiu observar a quantidade de alunos que apresentam todas as notas acima da média em todas as disciplinas. Para analisar melhor, a diretora Ana resolveu montar uma tabela com a quantidade de notas “azuis” em uma amostra de quatro turmas ao longo de um ano. Observe a seguir a tabela organizada pela diretora:

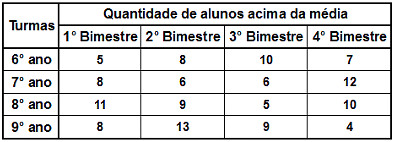
Antes de calcular a variância, é necessário verificar a média aritmética (x) da quantidade de alunos acima da média em cada turma:

6° ano → x = 5 + 8 + 10 + 7 = 30 = 7,50.
                  4               4

7° ano → x = 8 + 6 + 6 + 12 = 32 = 8,00.
                  4               4

8° ano → x = 11 + 9 + 5 + 10 = 35 = 8,75.
                    4              4

9° ano → x = 8 + 13 + 9 + 4 = 34 = 8,50.
                  4               4

Para calcular a variância da quantidade de alunos acima da média em cada turma, utilizamos uma amostra, por isso empregamos a fórmula da variância amostral:

Var. amostral = (x₁ – x)² + (x₂ – x)² + (x₃ – x)² + ... + (x_n – x)²
                       n – 1

6° ano → Var = (5 – 7,50)² + (8 – 7,50)² + (10 – 7,50)² + (7 – 7,50)²
                          4 – 1

Var = (– 2,50)² + (0,50)² + (2,50)² + (– 0,50)²
           3

Var = 6,25 + 0,25 + 6,25 + 0,25
         3

Var = 13,00
         3
Var = 4,33

7° ano → Var = (8 – 8,00)² + (6 – 8,00)² + (6 – 8,00)² + (12 – 8,00)²
                    4 – 1

Var = (0,00)² + (– 2,00)² + (– 2,00)² + (4,00)²
          3

Var = 0,00 + 4,00 + 4,00 + 16,00
         3

Var = 24,00
         3
Var = 8,00

8° ano → Var = (11 – 8,75)² + (9 – 8,75)² + (5 – 8,75)² + (10 – 8,75)²
                    4 – 1

Var = (2,25)² + (0,25)² + (– 3,75)² + (1,25)²
        3

Var = 5,06 + 0,06 + 14,06 + 1,56
         3

Var = 20,74
         3
Var = 6,91

9° ano → Var = (8 – 8,50)² + (13 – 8,50)² + (9 – 8,50)² + (4 – 8,50)²
                      4 – 1

Var = (– 0,50)² + (4,50)² + (0,50)² + (– 4,50)²
         3

Var = 0,25 + 20,25 + 0,25 + 20,25
           3

Var = 41,00
         3
Var = 13,66

Conhecida a variância de cada turma, vamos calcular agora o desvio padrão:

Para concluir sua análise, a diretora pode apresentar os seguintes valores que indicam a quantidade média de alunos acima da média por turma pesquisada:

6° ano: 7,50 ± 2,08 alunos acima da média por bimestre;
7° ano: 8,00 ± 2,83 alunos acima da média por bimestre;
8° ano: 8,75 ± 2,63 alunos acima da média por bimestre;
9° ano: 8,50 ± 3,70 alunos acima da média por bimestre;

Outra medida de dispersão é o coeficiente de variação. Veja aqui como calculá-lo!

Por Amanda Gonçalves
Graduada em Matemática