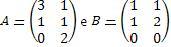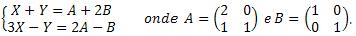Antes de adentrarmos nestes conceitos, vamos discutir o que caracteriza uma equação. Nela nos deparamos com três importantes elementos (operações, igualdade e incógnita), de modo que ao relacionarmos estes três elementos, buscaremos determinar o valor da incógnita que satisfaça aquela igualdade. Esta concepção continua para Equações Matriciais, com uma ressalva apenas: as incógnitas são matrizes.
Não pare agora... Tem mais depois da publicidade ;)
Para que este estudo seja compreendido com um bom aproveitamento, é aconselhável que você revise os tópicos sobre Adição e subtração de matrizes , Multiplicação de matrizes e Multiplicando um número real por uma matriz.
Veremos algumas resoluções de equações matriciais para que possamos compreender o processo realizado para obtenção da matriz solução.
Exemplo 1
Encontre a matriz X, que satisfaça a seguinte igualdade X-A=B, onde
Antes de darmos início ao uso das matrizes, utilizaremos a igualdade dada para isolarmos a nossa incógnita X.
Sendo assim, substituiremos as matrizes que conhecemos nesta equação a fim de encontrarmos a matriz X.
Exemplo 2
Se é possível resolvermos equações matriciais, por que não sistemas de equações matriciais? Vejamos um exemplo:
Determine as matrizes X e Y, que satisfaça o sistema a seguir.
Primeiramente devemos encontrar as relações de X e Y, através do sistema dado, para daí então iniciarmos o cálculo de cada matriz.
Sendo assim, temos duas relações para as matrizes solução.
.png)
Encontrando a matriz Y:
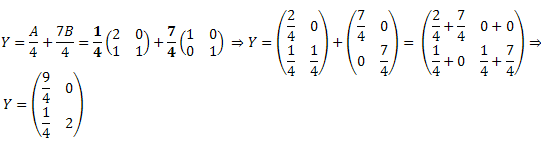
Encontrando a matriz X:
.png)
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola
Matriz e Determinante - Matemática - Brasil Escola
.jpg "Matrizes")