A equação paramétrica da reta é uma entre as diversas formas de se representar a reta de forma algébrica. Nela há uma equação para o valor de x e uma equação para o valor de y, ambas em função do mesmo parâmetro t. De modo geral, a equação paramétrica da reta é a equação tal que f(t) = x e g(t) = x, em que \(f(t)=x_0+at\) e \(g(t)=y_0+bt\).
Leia também: Ponto de interseção entre duas retas
Tópicos deste artigo
- 1 - Parâmetros
- 2 - Como calcular as equações paramétricas da reta?
- 3 - Exercícios resolvidos sobre a equação paramétrica da reta
Parâmetros
A equação paramétrica da reta é uma das maneiras de se representar a reta. Utilizamos como parâmetro uma variável t e reescrevemos as variáveis x e y em função do valor de t, logo, de modo geral, a equação paramétrica da reta é esta:
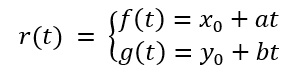
Os pontos pertencentes à reta, P(f(t), g(t)), satisfazem a equação paramétrica. Então, de modo geral, conhecendo a equação paramétrica, temos que r(t) = (\(x_0+at,y_0+bt\)). Para encontrar os pontos pertencentes à reta, basta atribuirmos valores para t.
Exemplo:
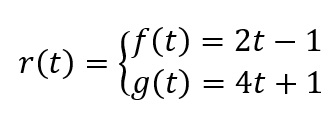
Conhecendo a equação paramétrica, podemos encontrar os pontos que pertencem a essa reta substituindo o valor de t.
Exemplo 1:
t = 1
\(f(1)=2⋅1-1=2-1=1\)
\(g(1)=4⋅1+1=4+1=5\)
Então o ponto A(1, 5) pertence à reta.
Exemplo 2:
t = -1
\(f(-1)=2⋅(-1)-1=-2-1=-3\)
\(g(-1)=4⋅(-1)+1=-4+1=-3\)
Então o ponto B(-3, -3) pertence à reta.
Como calcular as equações paramétricas da reta?
Conhecendo a equação geral da reta, é possível encontrar a equação paramétrica da reta, para isso, buscamos reescrever as duas variáveis em função de t.
Exemplo:
Escreva a equação paramétrica da reta 3x + 4y – 16 = 0.
Resolução:
Primeiro isolaremos a variável x:
\(3x=-4y+15\)
\(x=\frac{-4}{3} y+\frac{15}{3}\)
\(x=\frac{-4}{3} y+5\)
Note que o numerador da fração do coeficiente de y é -4. Para que seja possível colocar 4 em evidência, reescreveremos 5 como 4 + 1.
\(x=\frac{-4}{3} y+4+1\)
\(x=4(\frac{y}{3}+1)+1\)
Chamaremos \(\frac{y}{3}+1=t\), assim:
\(x=4t+1\)
Fazendo x = f(t), então \(f(t)=4t+1\).
Agora encontraremos g(t):
\(\frac{y}{3}+1=t\)
\(\frac{y}{3}=t-1\)
\(y=3t-3\)
Seja g(t) = y, então g(t) = 3t – 3.
Assim a equação paramétrica da reta é:
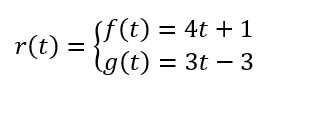
Podemos encontrar também a equação geral da reta por meio da equação parametrizada da reta. Para isso, isolaremos a variável t em uma das equações e substituir na outra.
Exemplo:
Encontre a equação geral da reta cuja equação paramétrica é:
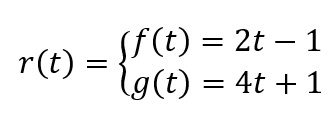
Sabemos que f(t) = x, então x = 2t – 1. Isolando o t, temos que:
\(x=2t-1\)
\(x-1=2t\)
\(t=\frac{x-1}2\)
Na outra equação, temos que g(t) = y.
\(y=4t+1\)
Substituindo t pelo valor isolado na primeira equação:
\(y=4⋅(\frac{x-1}{2})+1\)
\(y=2⋅(x-1)+1\)
\(y=2x-2+1\)
\(y=2x-1\)
Ao igualar a zero, encontraremos a equação geral da reta:
\(y-2x+1=0\)
Leia também: Equação reduzida da reta — um método que facilita a representação da reta no plano cartesiano
Exercícios resolvidos sobre a equação paramétrica da reta
Questão 1
Dada a reta de equação paramétrica r(t) = (2t – 3, 4t + 1), marque a alternativa que possui as coordenadas dos pontos da reta, cujo valor de t = 0,5.
A) A\((-1,-2)\)
B) A(1, \(-2\))
C) A(2, 3)
D) A(\(-2\), 3)
E) A( 3,\(-2\))
Resolução:
Alternativa D
As coordenadas desse ponto serão:
\(x=2⋅0,5-3\)
\(x=1-3\)
\(x=-2\)
Agora calculando y:
\(y=4⋅0,5+1\)
\(y=2+1\)
\(y=3\)
Então as coordenadas do ponto serão:
A(\(-2\), 3)
Questão 2
A equação geral da reta que possui equação paramétrica é:
A) 3y – 2x + 1 = 0
B) y + 2x – 2 = 0
C) y + x – 1 = 0
D) 2y – 3x + 3 = 0
E) y + 3x – 1 = 0
Resolução:
Alternativa E
Seja f(t) = x e g(t) = y, temos que:
x = t + 1
Isolando o t:
x – 1 = t
Substituindo t por x – 1 na equação g(t), temos que:
y = –3(x – 1) – 2
y = –3x + 3 – 2
y = – 3x +1
Igualando a zero, então a equação geral da reta será:
y + 3x – 1 = 0
Por Raul Rodrigues de Oliveira
Professor de Matemática

