A divisão de números complexos é uma operação entre números na forma \(a+bi\). Devido à estrutura desses números, a divisão entre complexos é calculada ao multiplicar-se o numerador e o denominador pelo conjugado do denominador. Também é possível fazer a divisão de números complexos na forma trigonométrica.
Leia também: Como calcular a divisão de polinômios?
Tópicos deste artigo
- 1 - Resumo sobre a divisão de números complexos
- 2 - O que são números complexos?
- 3 - Como calcular a divisão de números complexos?
- 4 - Divisão de números complexos na forma trigonométrica
- 5 - Exercícios sobre divisão de números complexos
Resumo sobre a divisão de números complexos
- A divisão de números complexos é uma operação entre números na forma \(a+bi\).
- Na prática, a divisão entre os números complexos \(z_1\) e \(z_2\) é calculada pelo produto do numerador e denominador na fração \(\frac{z_1}{z_2}\) do conjugado de \(\bar{z_2}\), expresso pelo como \(\bar{z_2}\). Portanto:
\(\frac{z_1}{z_2}=\frac{z_1}{z_2}\cdot\frac{\bar{z_2}}{\bar{z_2}}\)
- Seja \( r=\left|z\right|=\sqrt{a^2+b^2}\) e θ o ângulo entre o eixo horizontal (eixo real) e o segmento com extremidades em (0,0) e (a,b), a forma trigonométrica do número complexo \(z=a+bi\) é:
\(z=r\ \left(cos\ \theta+i\cdot s e n\ \theta\right)\)
- A divisão entre os números complexos z1 e z2 na forma trigonométrica é:
\(\frac{z_1}{z_2}=\frac{r_1\left(cos\theta_1+i\cdot s e n\theta_1\right)}{r_2\left(cos\theta_2+i\cdot s e n\theta_2\right)}=\frac{r_1}{r_2}\left[cos\left(\theta_1-\theta_2\right)+i\cdot s e n\left(\theta_1-\theta_2\right)\right]\)
O que são números complexos?
Os números complexos são números formados por uma parte real e por uma parte imaginária. Se a e b são números reais e \(i=\sqrt{-1}\) é a unidade imaginária, então um número complexo tem a forma:
\(z=a+bi\)
Nessa forma, a e b são reais e\(i=\sqrt{-1}\)é a unidade imaginária. Os coeficientes a e b são chamados, respectivamente, de parte real e parte imaginária do número complexo z.
Veja, a seguir, alguns exemplos de números complexos:
\(3, \ pois\ 3=3+0i\)
\(\frac{1}{2},\ pois\ \frac{1}{2}=\frac{1}{2}+0i\)
\(5+7i\)
\(9-6i\)
Um conceito importante dos números complexos é o conceito de conjugado. Dado um número complexo \(\bar{z}=a-bi\), chamamos o número complexo \(z=a+bi\) de conjugado de z. Utilizando a propriedade distributiva, que também é válida nesse caso, observamos que o produto entre um número complexo e seu conjugado é a soma dos quadrados dos coeficientes a e b:
\(z\cdot\bar{z}=\left(a+bi\right)\cdot\left(a-bi\right)=a^2+b^2\)
Como calcular a divisão de números complexos?
Para calcular a divisão de números complexos, considere os números complexos \(z_1=a_1+b_1i\) e \(z_2=a_2+b_2i\) . A divisão entre esses números é a razão:
\(\frac{z_1}{z_2}\)
Na prática, para calcular essa divisão, multiplicamos o numerador e o denominador pelo conjugado do denominador:
\(\frac{z_1}{z_2}=\frac{z_1}{z_2}\cdot\frac{\bar{z_2}}{\bar{z_2}}\)
Vejamos um exemplo de divisão de números complexos.
- Exemplo:
Determine a divisão entre os números complexos \(z_1=1+5i\) e \(z_2=3+2i\).
Resolução:
Devemos calcular o quociente de:
\(\frac{1+5i}{3+2i}\)
Como o conjugado de 3 + 2i é 3 - 2i, temos que:
\( \frac{1+5i}{3+2i}=\frac{1+5i}{3+2i}\cdot\frac{3-2i}{3-2i} \)
\(=\frac{3-2i+15i-10i^2}{3^2+2^2}\)
\(=\frac{13+13i}{13}\)
\(=1+i\)
Divisão de números complexos na forma trigonométrica
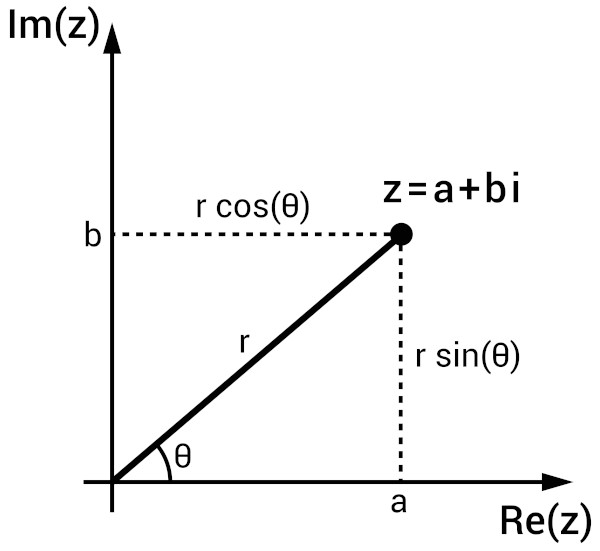
Para calcular a divisão de números complexos na forma trigonométrica, é preciso conhecer a forma trigonométrica de um número complexo. Dado um número complexo z = a + bi, sua forma trigonométrica é:
\(z=r\ \left(cos\ \theta+i\cdot s e n\ \theta\right)\)
Nessa forma, \(r=\left|z\right|=\sqrt{a^2+b^2}\) é o comprimento do segmento com extremidades na origem e no ponto (a,b) e θ é o ângulo entre o eixo horizontal e o segmento.
Considere dois números complexos escritos na forma trigonométrica:
\(z_1=r_1\left(cos\theta_1+i\cdot s e n\theta_1\right)\)
\(z_2=r_2\left(cos\theta_2+i\cdot s e n\theta_2\right)\)
A expressão da divisão entre z1 e z2, na forma trigonométrica, é:
\(\frac{z_1}{z_2}=\frac{r_1\left(cos\theta_1+i\cdot s e n\theta_1\right)}{r_2\left(cos\theta_2+i\cdot s e n\theta_2\right)}=\frac{r_1}{r_2}\left[cos\left(\theta_1-\theta_2\right)+i\cdot s e n\left(\theta_1-\theta_2\right)\right]\)
- Exemplo:
Calcule a divisão entre \(z_1=4\left(cos\frac{\pi}{2}+i\cdot s e n\frac{\pi}{2}\right)\) e \(z_2=3\sqrt2\left(cos\frac{\pi}{4}+i\cdot s e n\frac{\pi}{4}\right)\).
Resolução:
Aplicando a expressão para a divisão entre números complexos na forma trigonométrica, temos que:
\(\frac{z_1}{z_2}=\frac{4\left(cos\frac{\pi}{2}+i\cdot s e n\frac{\pi}{2}\right)}{3\sqrt2\left(cos\frac{\pi}{4}+i\cdot s e n\frac{\pi}{4}\right)}=\frac{4}{3\sqrt2}\left[cos\left(\frac{\pi}{2}-\frac{\pi}{4}\right)+i\cdot s e n\left(\frac{\pi}{2}-\frac{\pi}{4}\right)\right]\)
\(=\frac{4}{3\sqrt2}\left[cos\left(\frac{\pi}{4}\right)+i\cdot s e n\left(\frac{\pi}{4}\right)\right]\)
\(=\frac{4}{3\sqrt2}\left[\frac{\sqrt2}{2}+i\cdot\frac{\sqrt2}{2}\right]\)
\(=\frac{4}{3\sqrt2}\left[\frac{\sqrt2}{2}\left(1+i\right)\right]\)
\(=\frac{2}{3}+\frac{2}{3}i\)
Veja também: Como fazer a radiciação de números complexos na forma trigonométrica?
Exercícios sobre divisão de números complexos
Questão 1
A divisão entre os números complexos \(z_1=1+4i\) e \(z_2=-1+2i\) é igual a:
A) 1,2+1,4i
B) 1,2-1,4i
C) 1,4+1,2i
D) 1,4-1,2i
E) 1,4+1,4i
Resolução:
Alternativa D
Como \(\bar{z_2}=-1-2i\), temos que:
\(\frac{z_1}{z_2}=\frac{1+4i\ }{-1+2i\ }\cdot\frac{-1-2i}{-1-2i}\)
\(=\frac{-1-2i-4i-8i^2}{1^2+2^2}\)
\(=\frac{7-6i}{5}\)
\(1,4-1,2i\)
Questão 2
Qual o quociente entre os números complexos \(z_1=5\sqrt2\left(cos\frac{\pi}{4}+i\cdot s e n\frac{\pi}{4}\right)\ e \ z_2\)?
A) \( 2+5i\)
B) \( 2-5i\)
C) \( 2,5+2,5i\)
D) \( 5,2+5,2i\)
E) \( 2,5-2,5i\)
Resolução:
Alternativa E
Aplicando a expressão para a divisão entre números complexos na forma trigonométrica, temos que:
\(\frac{z_1}{z_2}=\frac{5\sqrt2\left(cos\frac{\pi}{4}+i\cdot s e n\frac{\pi}{4}\right)}{3\left(cos\frac{\pi}{2}+i\cdot s e n\frac{\pi}{2}\right)}=\frac{5\sqrt2}{3}\left[cos\left(\frac{\pi}{4}-\frac{\pi}{2}\right)+i\cdot s e n\left(\frac{\pi}{4}-\frac{\pi}{2}\right)\right]\)
\(=2,5\sqrt2\left[cos\left(-\frac{\pi}{4}\right)+i\cdot s e n\left(-\frac{\pi}{4}\right)\right]\)
\(=2,5\sqrt2\left(\frac{\sqrt2}{2}\cdot\left(1-i\right)\right)\)
\(=2,5-2,5i\)
Fontes
CARMO, M. P.; MORGADO, A. C.; WAGNER, E. Trigonometria Números Complexos. Coleção Professor de Matemática. São Paulo: SBM, 2005.
SILVA, F. G. L. da. Explorando as propriedades geométricas no ensino dos números complexos. Trabalho de Conclusão de Curso (Especialização em Ensino da Matemática no Ensino Médio) — Universidade Federal de Santa Maria, Santa Maria, 2016. Disponível em: https://repositorio.ufsm.br/handle/1/19340.


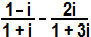 , na qual i é a unidade imaginária, é igual a:
, na qual i é a unidade imaginária, é igual a: