Velocidade vetorial

Velocidade vetorial é a medida com que uma certa distância é percorrida, durante um intervalo de tempo, quando levamos em conta parâmetros vetoriais, como módulo, direção e sentido. A velocidade vetorial pode ser calculada pelo vetor deslocamento — diferença entre os vetores de posição final e inicial — dividido pelo intervalo de tempo em que se deu o movimento.

Veja mais: Equilíbrio estático: quando a resultante das forças e a soma dos torques são nulas

Tópicos deste artigo

• 1 - Definição de velocidade vetorial
• 2 - Deslocamento vetorial
• 3 - Velocidade vetorial e velocidade escalar
• 4 - Velocidade vetorial média e instantânea
• 5 - Exercícios sobre velocidade vetorial

Definição de velocidade vetorial

Diferentemente da velocidade escalar, a velocidade vetorial média pode ser nula, mesmo que o corpo esteja em movimento. Isso acontece nos casos em que o móvel parte de uma posição e, ao final de um certo intervalo de tempo, retorna à mesma posição. Nesse caso dizemos que, mesmo que o espaço percorrido pelo móvel não tenha sido nulo, o deslocamento vetorial foi.movimento. pode ser nula, mesmo que o corpo esteja em, a velocidade vetorial média escalarDiferentemente da velocidade

A fórmula usada para calcular a velocidade vetorial de algum móvel é esta:

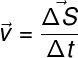
v – velocidade vetorial

ΔS – deslocamento vetorial

Δt – intervalo de tempo

Deslocamento vetorial

Chamamos de S_F e S₀, respectivamente, as posições em que o móvel encontrava-se ao final e início do movimento. Essas posições podem ser escritas na forma de pontos do plano cartesiano (x,y), para que possamos calcular o deslocamento vetorial, levando-se em conta a distância entre as coordenadas x e y de cada um dos pontos.

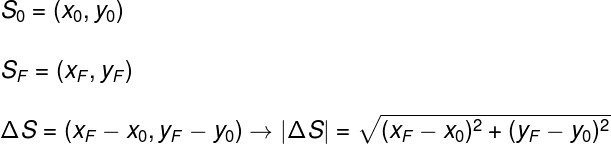
Outra forma de escrevermos o vetor deslocamento é por meio do uso de vetores unitários (um vetor que aponta nas direções x, y ou z e que tem módulo igual a 1). Os vetores unitários são usados para definir o módulo de cada componente do deslocamento ou da velocidade nas direções horizontal e vertical, representados pelos símbolos i e j, respectivamente.

Na figura seguinte, mostraremos as componentes do vetor deslocamento de um móvel que se encontrava na posição S₀ = 4,0i + 3,0j, e então se move para a posição S_F = 6,0i e 10,0j. O deslocamento, nesse caso, é dado pela diferença entre essas posições e é igual a ΔS = 2,0i + 7,0j.

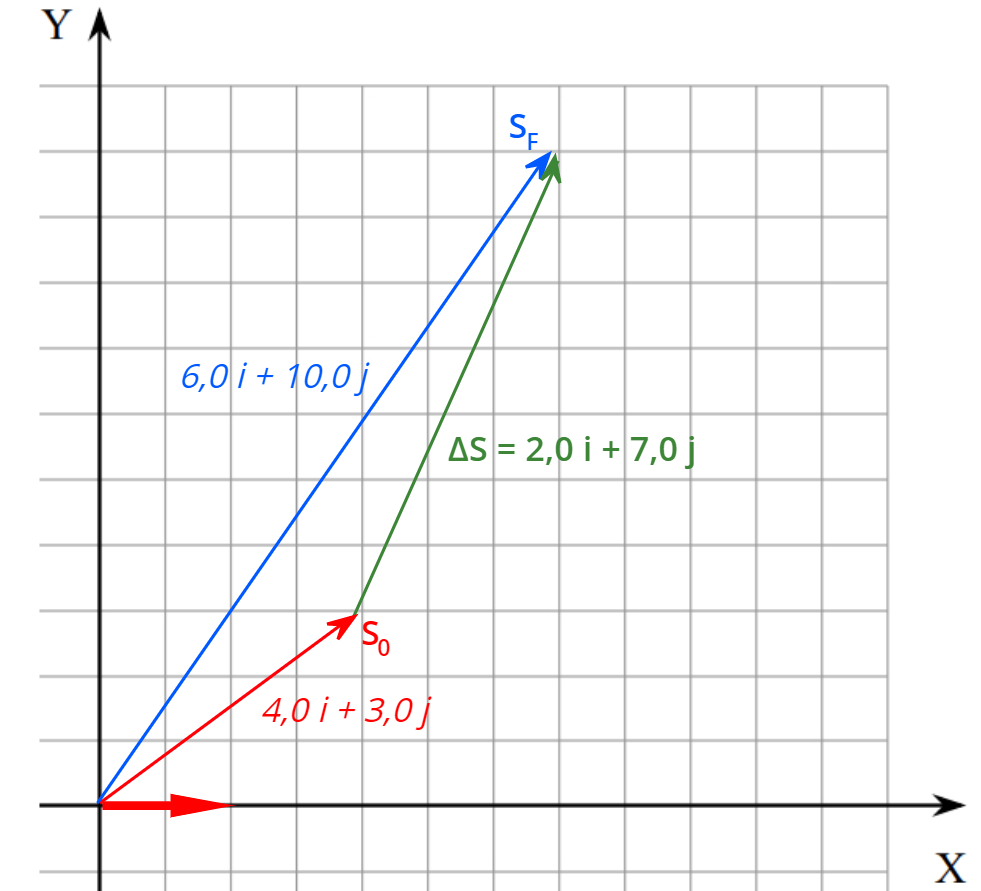
Conhecendo-se as componentes do vetor velocidade, é possível calcular o módulo do deslocamento, para tanto, devemos utilizar o teorema de Pitágoras, uma vez que essas componentes são perpendiculares entre si, observe:

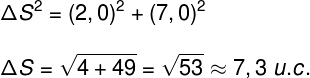
Depois de descobrirmos o módulo do vetor deslocamento, a velocidade vetorial poderá ser calculada dividindo-o pelo intervalo de tempo.

Veja mais: Força: agente da dinâmica responsável por alterar o estado de repouso ou movimento de um corpo

Velocidade vetorial e velocidade escalar

Como mencionado, a velocidade é uma grandeza vetorial, por isso, é definida com base em seu módulo, direção e sentido. Toda velocidade é vetorial, entretanto, grande parte dos livros didáticos usa o termo “velocidade escalar” para facilitar o estudo da cinemática para os estudantes do Ensino Médio. Dito isso, essa velocidade “escalar” é, na verdade, o módulo da velocidade vetorial de um móvel que se desloca ao longo de uma única direção do espaço.

Velocidade vetorial média e instantânea

Velocidade vetorial média é a razão entre o deslocamento vetorial e o intervalo de tempo em que esse deslocamento ocorre. Quando calculamos a velocidade média, o resultado obtido não indica que ela foi mantida durante todo o trajeto, podendo ter sofrido variações ao longo do tempo.

A velocidade instantânea, por sua vez, é definida para intervalos de tempo infinitesimais, ou seja, muito pequenos. A definição de velocidade vetorial instantânea remete, portanto, à medida da velocidade em cada instante:

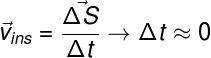
Exercícios sobre velocidade vetorial

Questão 1) (Mackenzie) Um avião, após deslocar-se 120 km para nordeste (NE), desloca-se 160 km para sudeste (SE). Sendo um quarto de hora o tempo total dessa viagem, o módulo da velocidade vetorial média do avião, nesse tempo, foi de:

a) 320 km/h

b) 480 km/h

c) 540 km/h

d) 640 km/h

e) 800 km/h

Gabarito: Letra e

Resolução:

As direções norte e nordeste são perpendiculares entre si, portanto, calcularemos o deslocamento vetorial desse avião utilizando o teorema de Pitágoras. Observe a figura seguinte que ilustra a situação descrita e o cálculo a ser realizado inicialmente:

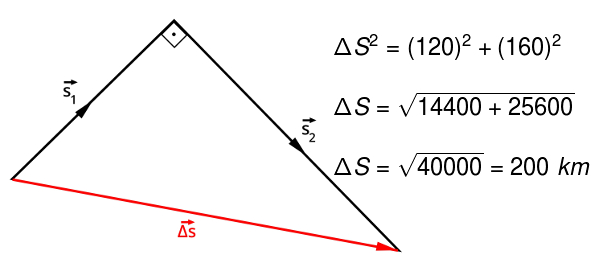
Depois de calcularmos o módulo do deslocamento vetorial, basta calcularmos a velocidade vetorial média, dividindo-a pelo intervalo de tempo, que é de ¼ de hora (0,25 h):

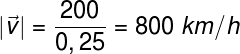
Com base nisso, descobrimos que a velocidade do avião é de 800 km/h, portanto, a alternativa correta é a letra e.

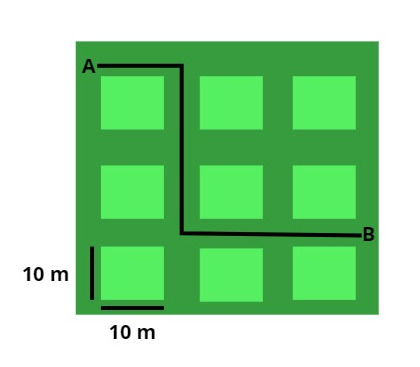
Questão 2) (Ufal) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago, era, em metros,

a) 680

b) 600

c) 540

d) 520

e) 500

Gabarito: Letra d

Resolução:

O exercício fala de dois deslocamentos perpendiculares. Para descobrirmos a distância entre os pontos final e inicial, devemos utilizar o teorema de Pitágoras, observe:

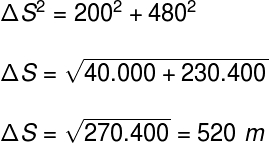
De acordo com o resultado obtido, a alternativa correta é a letra d.

Questão 3) (Uemg 2015) O tempo é um rio que corre. O tempo não é um relógio. Ele é muito mais do que isso. O tempo passa, quer se tenha um relógio ou não. Uma pessoa quer atravessar um rio num local onde a distância entre as margens é de 50 m. Para isso, ela orienta o seu barco perpendicularmente às margens. Considere que a velocidade do barco em relação às águas seja de 2,0 m/s e que a correnteza tenha uma velocidade de 4,0 m/s. Sobre a travessia desse barco, assinale a afirmação CORRETA:

a) Se a correnteza não existisse, o barco levaria 25 s para atravessar o rio. Com a correnteza, o barco levaria mais do que 25 s na travessia.

b) Como a velocidade do barco é perpendicular às margens, a correnteza não afeta o tempo de travessia.

c) O tempo de travessia, em nenhuma situação, seria afetado pela correnteza.

d) Com a correnteza, o tempo de travessia do barco seria menor que 25 s, pois ela aumenta vetorialmente a velocidade do barco.

Gabarito: Letra c

Resolução:

Independentemente da velocidade da correnteza, o tempo de travessia do barco será o mesmo, uma vez que a sua travessia dá-se de modo perpendicular às margens.

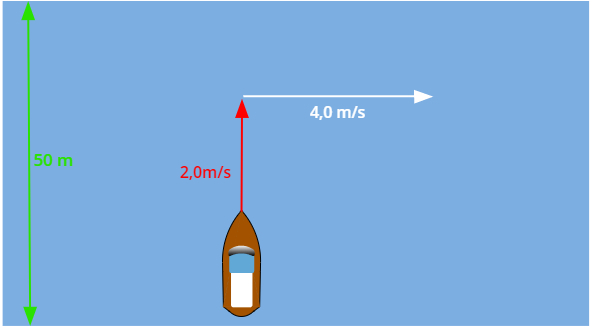
Entenda: a composição das duas velocidades do barco faz com que ele se mova na direção resultante delas, desse modo, a direção perpendicular ao rio, que tem 50 m de comprimento, é sempre percorrida pela velocidade do barco, que é de 2,0 m/s, e, por isso, o tempo de travessia não é afetado.

Por Rafael Helerbrock
Professor de Física