Equilíbrio estático

Equilíbrio estático é a condição em que a resultante das forças e a soma dos momentos das forças, ou torques, são nulas. Quando na situação de equilíbrio estático, os corpos encontram-se em repouso. Ao todo, existem duas três diferentes tipos de equilíbrio: estável, instável e indiferente.

Veja também: Tudo que você precisa saber sobre as leis de Newton

Tópicos deste artigo

• 1 - Equilíbrio estático e dinâmico
• 2 - Tipos de equilíbrio estático
• 3 - Equilíbrio do ponto material e equilíbrio do corpo extenso
• 4 - Exercícios resolvidos sobre equilíbrio estático

Equilíbrio estático e dinâmico

Antes de começarmos, alguns conceitos são de importância fundamental para compreendermos este artigo, confira quais são:

• Força resultante: é calculada por meio da 2ª lei de Newton. Na condição de equilíbrio, a soma vetorial dessas forças deve ser nula;
• Torque ou momento de uma força: diz respeito ao agente dinâmico da rotação, ou seja, quando se aplica um torque não nulo sobre um corpo, ele tenderá a descrever um movimento de rotação.

Chamamos de equilíbrio a situação em que um corpo, extenso ou puntual, está sujeito a uma força resultante nula. Desse modo, e de acordo com o que é estabelecido pela 1ª lei de Newton, conhecida como lei da inércia, um corpo em equilíbrio pode estar tanto em repouso quanto em movimento retilíneo uniforme — situações que são chamadas de equilíbrio estático e equilíbrio dinâmico, respectivamente.

Tipos de equilíbrio estático

• Equilíbrio instável: quando um corpo sofre um pequeno deslocamento de sua posição de equilíbrio, por menor que seja, ele tenderá a afastar-se cada vez mais dessa posição. Observe a figura a seguir:

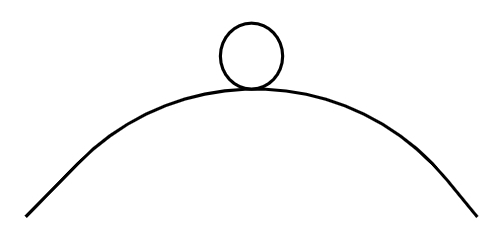
• Equilíbrio estável: quando um corpo, deslocado de sua posição de equilíbrio, tende a voltar para a sua posição inicial, como no caso mostrado nesta figura:

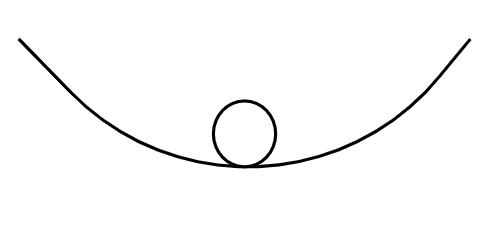
• Equilíbrio indiferente: quando um corpo, independentemente de onde seja posicionado, permanece em equilíbrio, confira:

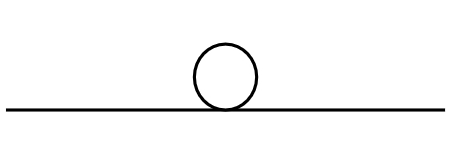
Saiba mais: Descubra como a bola de futebol faz curvas no ar

Equilíbrio do ponto material e equilíbrio do corpo extenso

Quando as dimensões de um corpo podem ser desprezadas, como no caso de uma pequena partícula, por exemplo, falamos em equilíbrio do ponto material. Nesses casos, para que o corpo esteja em equilíbrio, basta que o somatório das forças que atuam sobre ele seja nulo.

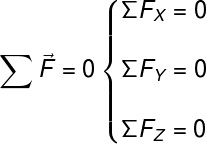
​F – força

F_X – componente x das forças

F_y – componente y das forças

Fz – componente z das forças

A figura indica que a soma das forças e a soma das componentes das forças em cada direção devem ser iguais a zero, para que o corpo de simetria puntual esteja em equilíbrio estático.

Quando não for possível desprezar as dimensões do corpo, como nos casos de barras, pontes levadiças, apoios, alavancas, engrenagens e outros objetos macroscópicos, fala-se em equilíbrio do corpo extenso. Para que se defina corretamente esse tipo de equilíbrio, é necessário levar em conta a distância entre o ponto de aplicação de uma força até o eixo de rotação desses corpos, em outras palavras, a condição de equilíbrio estático ou dinâmico exige que a somatória dos torques (ou momentos) seja nula, assim como ocorre com as forças aplicadas.

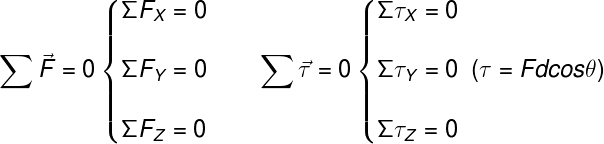
As condições anteriores indicam que, no caso de um corpo extenso, é necessário que a soma das forças e dos torques seja nula em cada uma das direções.

Exercícios resolvidos sobre equilíbrio estático

A resolução de exercícios sobre equilíbrio estático requer um conhecimento básico sobre soma vetorial e decomposição de vetores.

Acesse também: Está com dificuldades? Aprenda a resolver exercícios usando as leis de Newton

Questão 1) (Ifsul) Uma caixa A, de peso igual a 300 N, é suspensa por duas cordas B e C conforme a figura a seguir. (Dados: sen 30º = 0,5)

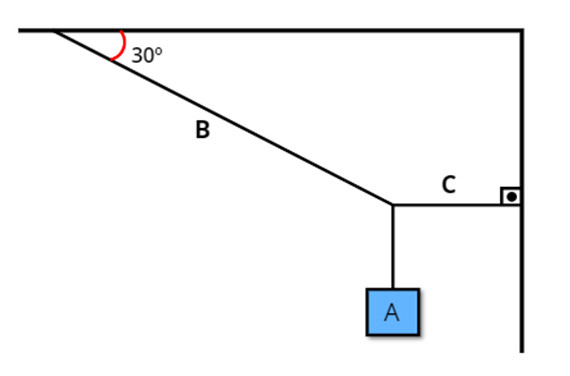
O valor da tração na corda B é igual a:

a) 150,0 N

b) 259,8 N

c) 346,4 N

d) 600,0 N

Gabarito: Letra d

Resolução:

Para resolvermos esse exercício, temos que utilizar a trigonometria, a fim de calcularmos a tração na corda B. Para isso, é necessário que usemos a definição de seno, pois o ângulo formado entre as cordas é de 30º, e a fórmula do seno indica que ele pode ser calculado pela razão entre o cateto oposto e a hipotenusa. Observe a próxima figura, nela formamos um triângulo com os vetores T_B (tração na corda B) e peso (P):

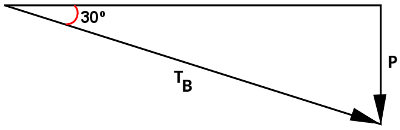
Com base nela, devemos fazer o seguinte cálculo:

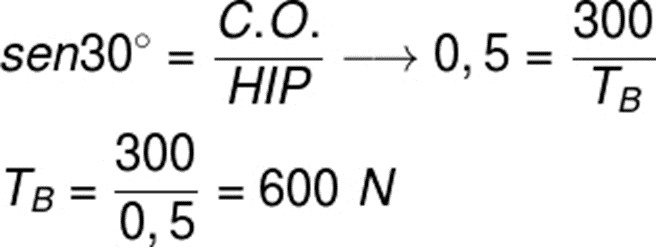
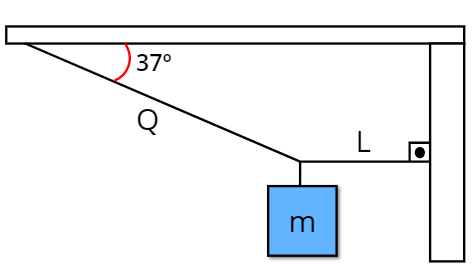
Questão 2) (Espcex) Um bloco de massa m = 24 kg é mantido suspenso em equilíbrio pelas cordas L e Q, inextensíveis e de massas desprezíveis, conforme figura a seguir. A corda L forma um ângulo de 90° com a parede e a corda Q forma um ângulo de 37° com o teto. Considerando a aceleração da gravidade igual a 10m/s², o valor da força de tração que a corda L exerce na parede é de:

(Dados: cos 37° = 0,8 e sen 37° = 0,6)

a) 144 N

b) 180 N

c) 192 N

d) 240 N

e) 320 N

Gabarito: Letra e

Resolução:

Primeiramente, devemos determinar qual é o valor da tração suportada pelo cabo Q, para tanto, usamos a relação do seno, como no exercício anterior:

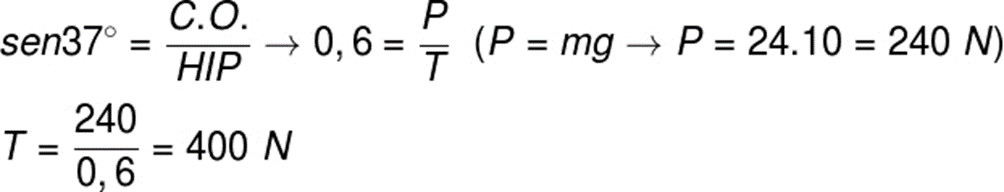
Depois de termos encontrado a tração no fio Q, devemos calcular a componente dessa tração que se cancela pela tração exercida pelo cabo L. Agora, usaremos o cosseno do ângulo, uma vez que a componente horizontal da tração no cabo Q é o cateto adjacente ao ângulo de 37º, observe:

Questão 3) (Uerj) Um homem de massa igual a 80 kg está em repouso e em equilíbrio sobre uma prancha rígida de 2,0 m de comprimento, cuja massa é muito menor que a do homem. A prancha está posicionada horizontalmente sobre dois apoios, A e B, em suas extremidades, e o homem está a  0,2 m da extremidade apoiada em A. A intensidade da força, em newtons, que a prancha exerce sobre o apoio A equivale a:

a) 200

b) 360

c) 400

d) 720

Gabarito: Letra D

Resolução:

Fizemos um esquema para que seja possível visualizar o exercício mais facilmente, confira:

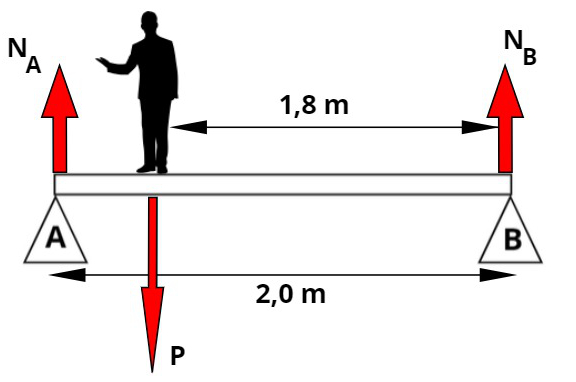
Como a barra em que o homem encontra-se apoiado é um corpo extenso, deve-se levar em conta tanto a soma das forças quanto a soma vetorial dos torques que atuam sobre ela. Desse modo, devemos fazer os seguintes cálculos:

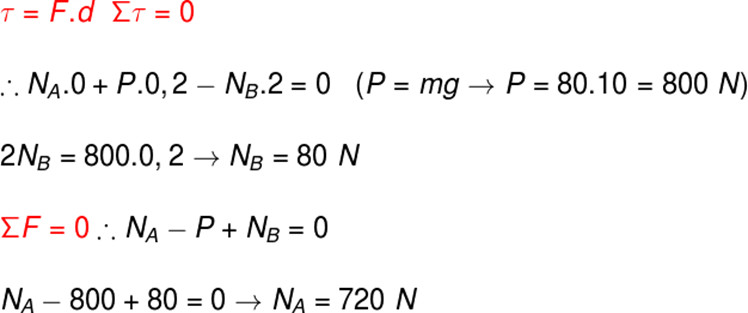
Para fazermos essas contas, primeiramente utilizamos a condição que afirma que a soma dos torques deve ser igual a zero, em seguida, multiplicamos as forças com as suas distâncias ao eixo de rotação da barra (no caso, escolhemos a posição A). Para a determinação dos sinais, utilizamos o sinal positivo para os torques que produzem rotações no sentido anti-horário, enquanto o sinal negativo foi utilizado para o torque produzido pela força peso, que tende a rotacionar a barra no sentido horário.

O cálculo da resultante dos torques resultou em N_B = 80 N, e, em seguida, utilizamos a segunda condição de equilíbrio. Nesse caso, dizemos que a soma das forças que atuam sobre a barra deve ser nula, e obtivemos uma reação normal no ponto A igual a 720 N.