MCU e MCUV: a principal diferença entre o movimento circular uniforme (MCU) e o movimento circular uniformemente variado (MCUV) é que no movimento circular uniforme, os corpos possuem a mesma velocidade escalar e velocidade angular durante todo o percurso circular, enquanto no movimento circular uniformemente variado a velocidade escalar e a velocidade angular dos corpos são alteradas durante o percurso circular.
Leia também: O que é aceleração?
Tópicos deste artigo
- 1 - Resumo sobre as diferenças entre MCU e MCUV
- 2 - O que é movimento circular uniforme (MCU)?
- 3 - O que é movimento circular uniformemente variado (MCUV)?
- 4 - Quais são as diferenças entre o MCUV e o MCU?
- 5 - Exercícios resolvidos sobre o MCU e o MCUV
Resumo sobre as diferenças entre MCU e MCUV
-
No movimento circular uniforme, temos apenas a aceleração centrípeta.
-
No movimento circular uniformemente variado, temos a aceleração centrípeta e a aceleração linear.
-
No movimento circular uniforme, as velocidades linear e angular são constantes.
-
No movimento circular uniformemente variado, as velocidades linear e angular não são constantes.
-
Curvas, rotações, funcionamento de engrenagens e roldanas são situações em que lidamos com o movimento circular.
Não pare agora... Tem mais depois da publicidade ;)
O que é movimento circular uniforme (MCU)?
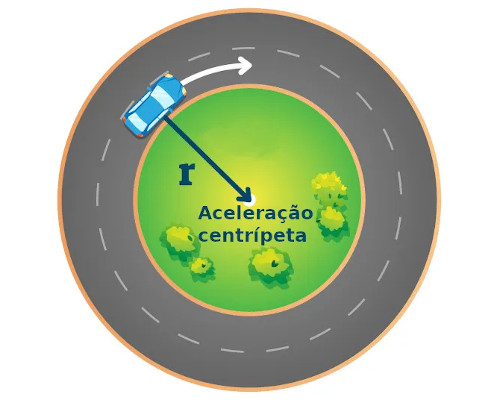
O movimento circular uniforme (MCU) é assim conhecido por descrever o movimento dos corpos ao longo de trajetórias circulares de raio constante com velocidade escalar e velocidade angular constantes.
Ainda que seja chamado de movimento uniforme em razão de o módulo da velocidade ser constante, ele se trata de um movimento acelerado, já que a orientação da velocidade é alterada pela aceleração centrípeta, aceleração que mantém os corpos na trajetória durante o movimento circular em razão da sua orientação radial para o centro da curva.
O que é movimento circular uniformemente variado (MCUV)?
O movimento circular uniformemente variado (MCUV) é assim conhecido por descrever o movimento dos corpos ao longo de trajetórias circulares de raio constante com velocidade escalar e velocidade angular variadas.
Trata-se de um movimento acelerado, já que possui uma aceleração centrípeta e uma aceleração linear com orientação tangencial ao movimento, que é responsável por alterar a velocidade linear e, consequentemente, a velocidade angular.
Quais são as diferenças entre o MCUV e o MCU?
Tanto o movimento circular uniformemente variado quanto o movimento circular uniforme são movimentos circulares, pois ocorrem em situações envolvendo curvas, rotações, engrenagens, roldanas etc.
Contudo, o movimento circular uniformemente variado apresenta variações nas intensidades das velocidades linear e angular devido às suas acelerações centrípeta e linear. Já no movimento circular uniforme, as suas velocidades linear e angular são constantes durante o movimento pelo fato de a aceleração centrípeta alterar apenas a orientação da velocidade, e não a sua intensidade, porque a responsável por isso, a aceleração linear, é nula.
Podemos calcular a aceleração centrípeta no MCU e MCUV por meio da fórmula:
\(a_{cp}=\frac{v^2}R\)
-
\(a_{cp}\) é a aceleração centrípeta, medida em \([m/s^2] \).
-
v é a velocidade linear, medida em \( [m/s]\)
-
R é o raio da circunferência.
Como a aceleração linear no MCU é nula, no MCUV podemos calculá-la por meio da fórmula:
\(a=α\cdot R\)
-
α é a velocidade angular, medida em \([rad/s^2] \).
-
a é a aceleração linear, medida em \([m/s^2] \).
-
R é o raio da circunferência.
Leia também: Aceleração angular — grandeza que descreve a velocidade angular em uma trajetória circular
Exercícios resolvidos sobre o MCU e o MCUV
Questão 1
Qual a aceleração linear de um móvel que percorre uma circunferência com raio de 0,4 m e com uma aceleração angular de \(1,25\ rad/s^2\)?
a) \(0,5\ m/s^2\).
b) \(1,0\ m/s^2\).
c) \(1,5\ m/s^2 \).
d) \(2,0\ m/s^2 \).
e) \(2,5\ m/s^2 \).
Resolução:
Alternativa A.
Calcularemos a aceleração linear por meio da sua relação com a aceleração angular e o raio:
\(a=α\cdot R\)
\(a=1,25\cdot 0,4\)
\(α=0,5\ m/s^2\)
Questão 2
Qual a aceleração centrípeta de um móvel que percorre uma circunferência com raio de 10 m e com uma velocidade linear de 50 m/s?
a) \(62,5\ m/s^2\)
b) \(125\ m/s^2\)
c) \(250\ m/s^2\)
d) \(500\ m/s^2\)
e) \(1000\ m/s^2\)
Resolução:
Alternativa C.
Calcularemos a aceleração centrípeta utilizando a sua fórmula:
\(a_{cp}=\frac{v^2}R\)
\(a_{cp}=\frac{50^2}{10}\)
\(a_{cp}=\frac{2500}{10}\)
\(a_{cp}=250\ m/s^2\)
Por Pâmella Raphaella Melo
Professora de Física

