O movimento circular uniformemente variado, ou simplesmente MCUV, é um movimento acelerado em que uma partícula se move ao longo de uma trajetória circular de raio constante. Diferentemente do movimento circular uniforme, no MCUV, há, além da aceleração centrípeta, uma aceleração angular, responsável por uma variação na velocidade em que o ângulo é percorrido.
O movimento circular uniformemente variado pode ser compreendido mais facilmente se conhecemos as equações horárias do MUV, uma vez que as equações do MCUV são similares a elas, mas são aplicadas a grandezas angulares.
Veja também: Movimento circular uniforme (MCU) — conceitos, fórmulas, exercícios
Tópicos deste artigo
MCU e MCUV
MCU e MCUV são movimentos circulares, entretanto, no MCU, a velocidade angular é constante e não há aceleração angular. Já no MCUV, a velocidade angular é variável, em razão de uma aceleração angular constante. Apesar de ser chamado de movimento circular uniforme, o MCU é um movimento acelerado, visto que em ambos existe uma aceleração centrípeta, que faz com que uma partícula desenvolva uma trajetória circular.

Teoria do MCUV
Como dissemos, o MCUV é aquele em que uma partícula desenvolve uma trajetória circular de raio constante. Além da aceleração centrípeta, responsável por mudar constantemente a direção da velocidade tangencial da partícula, há também uma aceleração angular, medida em rad/s². Essa aceleração mede a variação da velocidade angular e, por se tratar de um movimento uniformemente variado, apresenta módulo constante.
As equações do MCUV são similares às equações do movimento uniformemente variado (MUV), no entanto, em vez de usarmos equações horárias de posição e de velocidade, utilizamos as equações horárias angulares.
Veja também: Mecânica – tipos de movimento, fórmulas e exercícios
Fórmulas do MCUV
As fórmulas do MCUV são fáceis de entender, se você já compreende o movimento uniformemente variado. Para cada uma das fórmulas do MUV, há uma correspondente no MCUV. Observe:
![]()
vF e v0 – velocidades final e inicial (m/s)
ωF e ω0 – velocidades angulares final e inicial (rad/s)
a – aceleração (m/s²)
α – aceleração angular (rad/s²)
t – instante de tempo (s)
Acima mostramos as funções horárias da velocidade, respectivamente, relacionadas ao MUV e ao MCUV. A seguir observamos a função horária da posição para cada um desses casos.
![]()
SF e S0 – posições final e inicial (m)
ΘF e Θ0 – posição angular final e inicial (rad)
Além das duas equações fundamentais, mostradas anteriormente, há também a equação de Torricelli para o MCUV. Veja:
![]()
ΔS – deslocamento espacial (m)
ΔΘ – deslocamento angular (rad)
Há ainda uma fórmula que é utilizada para calcular explicitamente a aceleração angular do movimento, a saber:
![]()
Agora que já conhecemos as principais fórmulas do MCUV, precisamos fazer exercícios. Vamos lá?
Veja também: Sete dicas de "ouro" para estudar Física por conta própria e se dar bem nas provas!
Exercícios resolvidos sobre o MCUV
Questão 1 — Uma partícula move-se ao longo de uma trajetória circular de raio igual a 2,5 m. Sabendo que, em t = 0 s, a velocidade angular dessa partícula era de 3 rad/s e que, no instante t = 3,0 s, sua velocidade angular era igual a 9 rad/s, a aceleração angular dessa partícula, em rad/s², é igual a:
a) 2,0 rad/s².
b) 4,0 rad/s².
c) 0,5 rad/s².
d) 3,0 rad/s².
Resolução:
Vamos calcular a aceleração angular dessa partícula. Observe o cálculo a seguir:
![]()
Com base no cálculo, descobrimos que a aceleração angular dessa partícula é de 2 rad/s², portanto a alternativa correta é a letra A.
Questão 2 — Uma partícula desenvolve um MCUV a partir do repouso, acelerando a uma taxa de 2,0 rad/s². Determine a velocidade angular dessa partícula no instante de tempo t = 7,0 s.
a) 7,0 rad/s
b) 14,0 rad/s
c) 3,5 rad/s
d) 0,5 rad/s
Resolução:
Para respondermos a essa questão, vamos utilizar a função horária da velocidade no MCU. Observe:
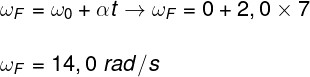
De acordo com o nosso cálculo, a velocidade angular da partícula no instante t = 7,0 s é igual a 14,0 rad/s, portanto a alternativa correta é a letra B.
Por Rafael Helerbrock
Professor de Física